What are forces ? – Quantum Bits

This question stems from discussions at work about the notion of “data gravity”, which, 10 years after its inception, seems to make a comeback and draw some kind of vague buzz within the Data & IT community. It quickly turned out that this concept – though appealing from afar – is one of these so many crackpot concepts that Wolfgang Paul would call “not even wrong“.

Indeed, the concept relies on misconceptions about sciences & physics in general, and the way (gravity) forces works and behaves in particular. McCrory’s “gravity formula” (which, somehow, tries to mimic Newton’s law of gravity) reminded me of one of my high school physics teacher’s favorite saying: “don’t mix elephants and wild strawberries in a formula !” (“Vous mélangez les éléphants et les fraises de bois !“).

So, let’s forget “data gravity” and … let’s go back to basics: what are forces ?

What are forces ?

Let’s first have a look at the etymology of the word: “force” comes from Middle English “force“, which comes from the Old French word “force” … which comes for latin “fortia” : strong, brave, courageous.

By extension, “force” describe any capacity of exercising an influence or producing an effect. “Force” is therefore a relatively ill-defined concept. But, at the same time, is also a highly intuitive notion: in this definition, “force” is related only to strength, and strength is something that anybody can immediately feel and experience.

Historically speaking, it took a long time to clearly define the concept, by relating forces not to strength, but to motion.

Following this path, philosophers such as Aristotle or early scientists such as Archimedes retained nevertheless fundamental errors in understanding force, due to an inadequate view of frictions and of the nature of natural motion: the belief – at the time – was that a force is required to maintain motion (even at a constant velocity).

Aristotelian physics began facing criticism in medieval science, but its shortcomings would not be fully corrected until the 17th century with physicists like Galileo Galilei or Sir Isaac Newton: a force is any interaction that will change the motion of an object. Using mathematics, Newton formulated his laws of motion, that were not improved for nearly three hundred years.

This all changed in the early 20th century, where observations lead physicists to completely new insights, giving birth to relativity and quantum mechanics.

Skipping Aristotelian physics, in the next paragraphs, we will explore the notion of force, within the historical framework of Newtonian physics and within the frameworks of today’s physics.

Newtonian physics

Laws of movement were set out in 1687 in Newton’s masterpiece “Philosophiae naturalis principia mathematica“. These three laws are the principles underlying the movement of bodies (i.e., what is now called classical mechanics). They describe the relationship between a body and the forces acting upon it, and its motion in response to those forces. They are completed with the law of universal gravitation (i.e. what is now called classical gravity).

Newton’s first law is the following (inertia principle): “Every body persists in its state of being at rest or of moving uniformly straight forward, except insofar as it is compelled to change its state by force impressed.”

In other terms, a particle not subject to forces moves (related to inertial frame) in a straight line at a constant speed. This is known as uniform motion:

An object that is at rest will stay at rest unless a force acts upon it.
An object that is in motion will not change its velocity unless a force acts upon it.

Newton’s first law can be mathematically summarized as:

Newton’s second law is the following (law of dynamics): “The alteration of motion is ever proportional to the motive force impress’d; and is made in the direction of the right line in which that force is impress’d“

In other terms, the second law states that the rate of change of momentum of a body is directly proportional to the force applied, and this change in momentum takes place in the direction of the applied force:

If we are considering a mass-contant system, $m$ can be taken out of the differentiation, and the second law can be expressed in terms of acceleration:

The net force applied to a body produces a proportional acceleration:

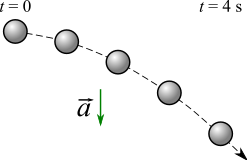
Newton’s second law enables one to calculate the equation of motion $x(t)$ , by integration of $\displaystyle \vec{a}={d^2\vec{x}}/{dt^2}$ .

Newton’s third law is the following (action-reaction): “To every action there is always opposed an equal reaction: or the mutual actions of two bodies upon each other are always equal, and directed to contrary parts.“

All forces occur in pairs such that if one object exerts a force on another object, then the second object exerts an equal and opposite reaction force on the first.

Newton’s laws gives a qualitative definition of the notion of force, and quantitatively relates force to motion via the acceleration of the body (i.e. its change of speed).

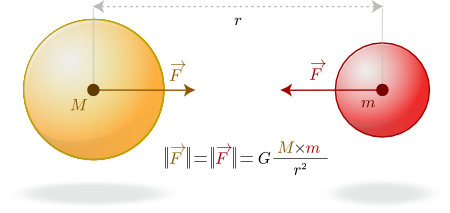
Let’s now introduce Newton’s law of universal gravitation: every body attracts every other body with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers.

In mathematical terms, the gravitational force between two bodies is

$\displaystyle \vec{f}= G \frac{m \times M}{r^2} \hat{r}$ ,

where $m$ and $M$ the messages of the bodies, $G$ is the gravitational constant, and $r$ the distance between them.

In the case of a N-body problem (N particles each interacting with each other due to gravity), applying the law of universal gravitation and Newton’s second law leads to a set of N nonlinear coupled second order ODEs:

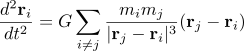
where $i = 1, 2,\cdots, N$ labels the quantities (mass, position, etc.) associated with each particle.

Solving these ODE’s leads to amazing trajectories:

Let’s pause a moment to think about what we have been able to do: Newton’s laws enabled us to formulate equations of motion (and trajectories, i.e. solutions of these equations) through the evaluation of forces, which makes them an extremely practical concept. Now, a question remains: are forces real physical objects, or just a tricks that enable calculations. As a matter of fact:

- When equating both $\vec{f}$ ‘s (the one from the second law and the one from law of universal gravity), $\vec{f}$ disappears from the resulting equations of motion;
- We could have formulated the same physics within the framework of Lagrangian mechanics, resulting of course with the same equations of motion, without ever introducing the concept of force: introducing instead kinetic energy $T$ and potential energy $V$ to define the Lagrangian, and using the principle of least action to derive the Euler-Lagrange equations:

$\displaystyle L = T - V,\ \ V = - G\ \frac{M\times m}{r},\ \ \frac {\partial {L}}{\partial q}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial {L}}{\partial {\dot {q}}}}\right)=0$

Of course, there is a very strong connection between forces and potential energy, and all this is could be seen as some kind of sleight of hand. Indeed, both formulations (Newton’s and Lagrange’s) are perfectly adequate when speaking in the words of classical physics.

Trouble is: Nature is NOT classical.

Even if the concept of force is easier to grasp than the one of potential energy (or field) in the conceptual framework of classical physics, it’ll be quite different when dealing with quantum and relativistic phenomena.

Modern physics (part 1): special and general relativity

As we have previously seen :

in absence of external influence, a free body follows a straight line at constant speed
under the influence of gravity, the body follows a trajectory explained by the combination of Newton’s second law of motion and Newton’s law of universal gravitation:

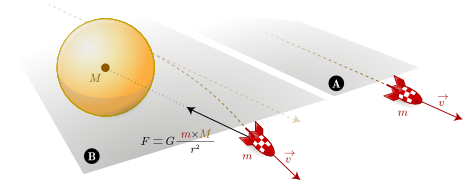
But major concerns (experimental and theoretical) lead physicists to seek for a totally new paradigm:

Newton’s theory cannot cope with today’s high precision observations. For example, it doesn’t fully explain the precession of the perihelion of the planet Mercury, or the deflection of light rays by gravity. In simple words: Newton’s gravity does not fit experimental observations.
Newton requires forces to be some kind of action at a distance, transmitted instantaneously, which is known now to be impossible: no information can travel faster than light.

To solve these problem, Einstein introduced its General Relativity theory, where effects of gravitation are ascribed to spacetime curvature instead of a force.

Einstein proposed that spacetime is curved by matter, and that free-falling objects are moving along locally straight paths in curved spacetime. These straight paths are called geodesics. In absence of gravity, physics is described by Einstein’s Special Relativity where geodesics are plain straight lines.

Einstein postulated that spacetime is a (pseudo-riemannian) manifold. Simply speaking, these are curved spaces which can always be locally approximated by flat pseudo-euclidean spaces (Minkowski spacetimes).

To deal with these geometry, one has to introduce new mathematical objects: tensors. Simply speaking, tensors are geometric entities that extend the notion of scalars, vectors and matrices. These are the natural objects to describe quantities in a relativistic way: tensors themselves are independent of a particular choice of coordinate system.

To express his field equations, Einstein introduced a particular tensor, denoted $T^{\mu\nu}$ and called stress-energy tensor. It is a quantity that describes the density and flux of energy and momentum in spacetime.

Then, he connected stress-energy tensors to local properties of spacetime (curvatures):

$\displaystyle G_{\mu\nu} + \Lambda g_{\mu\nu} = \frac{8\pi G}{c^4} T_{\mu\nu}$ where $\displaystyle G_{\mu\nu} = R_{\mu\nu} - \frac{1}{2} Rg_{\mu\nu}$

Theses field equations mean that energy / mass and momentum proportionally curves spacetime. In absence of gravity (A), spacetime is a flat Minkowskian manifold and free bodies follows straight line. In presence of gravity (B), spacetime is curved and free bodies follow geodesics:

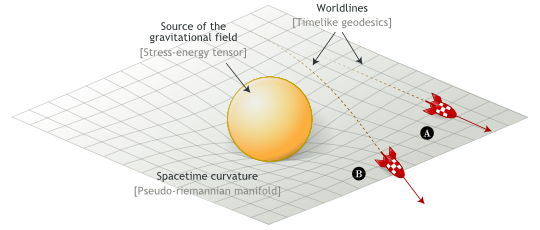
This is a huge paradigm shift: instead of thinking of gravity as a force pulling or pushing objects (instantaneous action at a distance), hence causing them to travel along curved paths in a 3-dimensional flat space, one has to think of objects traveling along the straightest paths (geodesics) in a 4-dimensional spacetime curved by the presence of energy and momentum.

And here come the unavoidable conclusion: there is no need for forces. Gravity manifest itself as a geometrical property of spacetime. When it comes to gravity, the concept of force is a meaningless.

Modern physics (part 2): quantum mechanics and particle physics

In particle physics, fundamental interactions are the ways that elementary particles interact with one another. An interaction is fundamental when it cannot be described in terms of other interactions. With the notable exception of gravitation (previously described though the framework of General Relativity), all these fundamental interactions have been expressed according to quantum field formulations, namely:

Quantum Electrodynamics (or QED): the quantum field formulation of electromagnetism, which served as a model for all the other theories
Quantum Chromodynamics (or QCD): the quantum field formulation of strong interactions (which used to be my playground in a distant past)
Electroweak model (or GWS): Sheldon Glashow, Steven Weinberg and Abdus Salam have unified both weak and electromagnetism interactions into a single, unified quantum theory, which is now the basis of the standard model of particle physics

Modern physical theories describe reality in terms of fields (e.g., the electromagnetic field, the gravitational field). Interactions are mediated by gauge boson, which are bosonic particle that carries any of the fundamental interactions.

Elementary particles interact with each other by the exchange of specific boson carriers:

Photons: carriers of the electromagnetic force
Gluons: the 8 gluons, are bosons that act as the exchange particles for the force between quarks (and actually, between gluons, which makes QCD a fun and tricky theory)
$W^{+}, W^{-}$ and $Z^0$ bosons: these bosons mediate the weak interaction

How can we picture these carriers ? Let’s forget for a minute fields and particles, and imagine a pair of basketball players (seen from above):

At first, let them separately dribble. Each player will follow his path, independently of the another. They are “non interacting players”. Now, imagine them exchanging a ball. Both players will now follow correlated path. They are “interacting players”. Then, give them an heavier ball. Their paths will get closer, because the range of their interaction will became shorter: exchanging an heavy ball over a long distance is harder than with a lighter one.

That’s about the same for particles. Electrically charged particle interact with each other by the exchange of virtual photons, quarks (color-charged particles) interact with each other by the exchange of virtual gluons, etc.

Instead of images of basketball players, physicists picture these interactions with Feynman diagrams (which, actually, are graphical representations of a perturbative contribution to a probability amplitude of a given quantum system):

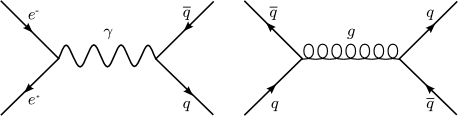
To summarize, quantum field theories describe the exchanges between elementary particles in the form of photons, bosons and gluons. Neither of these theories uses force.

Modern physics (part 3): symmetries and conservation laws

Symmetries and laws of physics are deeply connected. There exists an extremely important result called Noether’s theorem, which states that such symmetries also imply the conservation of physical quantities.

For example, energy is conserved if the laws describing a system at a given time are still the same at another time: time-translation invariance of the laws of physics implies the conservation of energy. The same link exists between conservation of (linear) momentum and space-translation invariance, or between conservation of angular momentum and rotations.

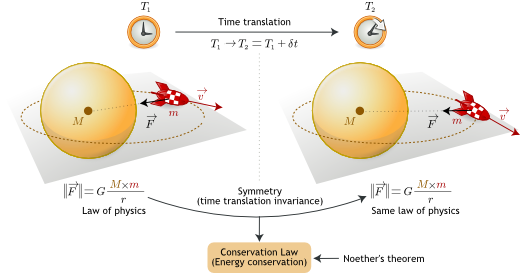
Symmetry principles are not just statements about how scientists should write laws. They make testable predictions about how nature behaves. Conversely, they constitute a formidable tool to formulate physical theories from experimental data: what truly and only characterize a physical system is what doesn’t change when one changes his point of view of that system.

Force is a redundant concept arising from conservation of momentum (4-momentum in relativity and momentum of virtual particles in quantum electrodynamics). The conservation of momentum can be directly derived from the homogeneity or symmetry of space and so is considered more fundamental than the concept of a force.

While moments or energy are fundamental quantities of physics, in the sense that they all obey a law of conservation, force can be seen as an artifice of modeling, convenient but not essential.

Leave a Reply Cancel reply