On topological quantum computers

We have been talking about quantum computing for a few weeks now. We have talked about its theoretical principles (quantum entanglement, no-cloning theorem, …) and its applications, especially in the contexts of cryptography and complexity. Yet, we haven’t talk much about practicalities.

The outstanding problem with entangled superpositions of spinning electrons, polarized photons or most other particles that might serve as qubits is that they are very unstable: even a slight interaction with the environment will collapse qubit’s superposition, forcing it into a definite state of $|0\rangle$ or $|1\rangle$ . This effect, called decoherence, abruptly ends quantum computations. Decoherence arises when the quantum system that encodes the qubits becomes entangled with its environment, which is a bigger, uncontrolled system.

We have already introduced these problems when speaking about quantum error correction: to fight decoherence, one has to completely isolate the computer from its environment, and careful eliminate of noise, and protocols for quantum correction of unavoidable errors. For this, a quantum computer requires each unit of information to be shared among an elaborate network of many qubits cleverly arranged to prevent an environmental disturbance of one from leading to the collapse of them all. Enormous progress has been achieved in this direction, but, to quote John Preskill: “That gives you a big overhead cost. If you want a hundred logical qubits you’d need tens of thousands of physical qubits in the computer.”

In 1997, having this problem in mind, Russian physicist Alexei Kitaev imagined a different approach to quantum computing: stable qubits could theoretically be formed from pairs of hypothetical particles called “non-abelian anyons”. He imagined a topological quantum computer built on anyons, whose world lines pass around one another to form braids in a three-dimensional spacetime (one temporal plus two spatial dimensions). In this approach, the state of a pair of non-abelian anyons is determined by its topology: how the paths of the two anyons have been braided around each other. If their paths are thought of as shoelaces meandering through space and time, then when the particles rotate around each other, the shoelaces tie in knots (illustration from Wikipedia):

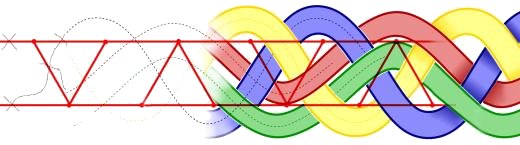
Small, cumulative perturbations can cause quantum states based on spin or polarization to decohere and introduce errors in the computation, but such small perturbations do not change the braids’ topological properties. In his model, Kitaev thought that these braids could be used to form the logic gates that make up his topological quantum computer.

What is topology ?

The motivating insight behind topology is that some geometric problems depend not on the exact shape of the objects involved, but rather on the way they are put together. For example, the square and the circle have many properties in common: they are both one dimensional objects (from a topological point of view) and both separate the plane into two parts, the part inside and the part outside.

Intuitively, topology is concerned with the properties of space that are preserved under continuous deformations (such as stretching and bending, but not tearing or gluing).

Topology is formally defined as the study of qualitative properties of certain objects (topological spaces) that are invariant under a certain kind of transformation (continuous map), especially those properties that are invariant under a certain kind of invertible transformation (homeomorphism). Important topological properties include connectedness and compactness.

A traditional joke is that a topologist cannot distinguish a coffee mug from a donut (it is said that they are topologically equivalent), since a sufficiently pliable donut could be reshaped to a coffee cup by creating a dimple and progressively enlarging it, while shrinking the hole into a handle (from Wikipedia):

As such, homeomorphism can be considered the most basic topological equivalence. Another one is the homotopy equivalence. Two continuous functions from one topological space to another are called homotopic if one can be “continuously deformed” into the other. Such a deformation is called a homotopy between the two functions. In the following figure, the two dashed paths shown above are homotopic relative to their endpoints and the animation represents one possible homotopy (from Wikipedia):

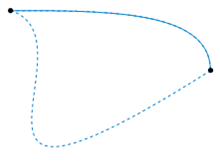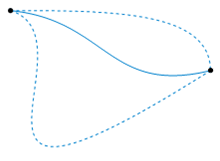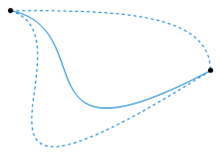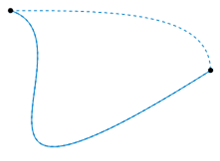
What are braids ?

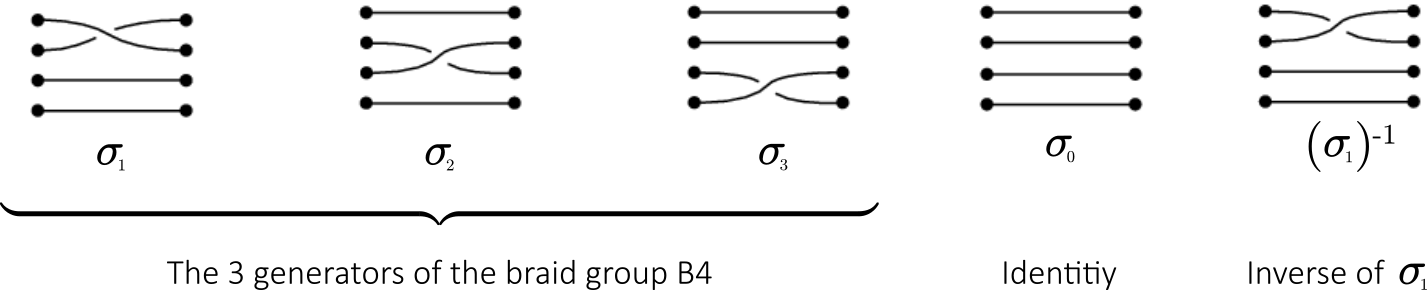
In topology, braid theory is an abstract geometric theory studying the concept of braid. The idea is that braids can be organized into groups, in which the group operation is “do the first braid on a set of strings, and then follow it with a second on the twisted strings”.

A braid group on $n$ strands (denoted $B n$ ) is the group whose elements are equivalence classes of n-braids, and whose group operation is composition of braids.

In this introduction we will set n = 4 (the generalization to other values of n is straightforward). Let’s consider two sets of four items lying on a table, with the items in each set being arranged in a vertical line, and such that one set sits next to the other. In the following illustration, these will be figured as black dots.

Using our four strands, each item of the first set is connected with an item of the second set so that a one-to-one correspondence results. Such a connection is called a braid.

Often some strands will have to pass over or under others, and this is crucial. The following two connections are different braids:

On the other hand, two such connections which can be made to look the same by “pulling the strands” are considered the same braid:

All strands are required to move from left to right. Knots like the following are not considered braids:

Any two braids can be composed by drawing the first next to the second, identifying the four items in the middle, and connecting corresponding strands:

The set of all braids on four strands is denoted by $B 4$ . The above composition of braids is a group operation. The identity element is the braid consisting of four parallel horizontal strands, and the inverse of a braid consists of that braid which “undoes” whatever the first braid did, which is obtained by flipping a diagram such as the ones above across a vertical line going through its center:

What are anyons ?

In space of three or more dimensions, elementary particles are either fermions or bosons: fermions obey Fermi–Dirac statistics, while bosons obey Bose–Einstein statistics.

In the language of quantum mechanics, for a 2-particle state with indistinguishable particles P1 and P2 of states $|\psi_1\rangle$ and $|\psi_2\rangle$ :

$|\psi_1 \psi_2\rangle = +|\psi_2 \psi_1\rangle\$ for bosons;
$|\psi_1 \psi_2\rangle = -|\psi_2 \psi_1\rangle\$ for fermions;

In a 2-dimensional world, however, things are different. Let’s have a look at the following diagrams:

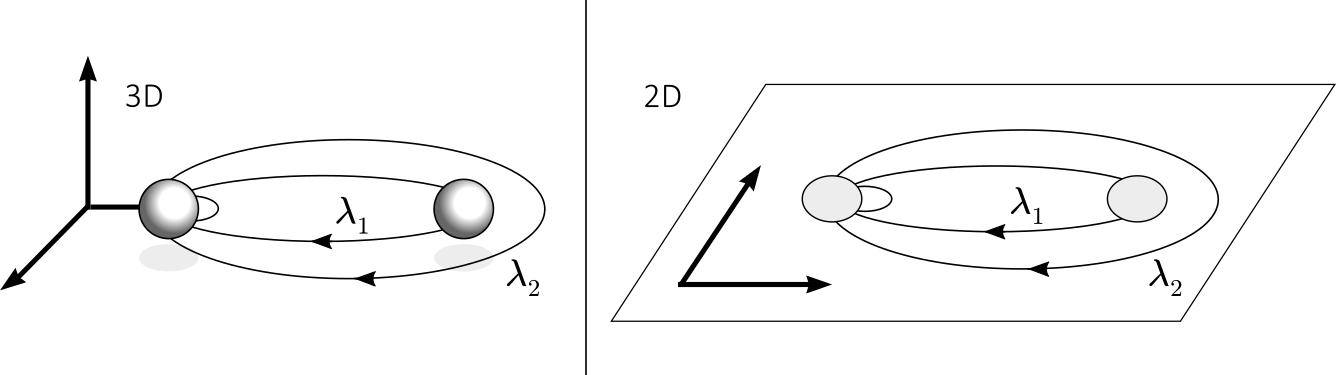
In a 3-dimensionnal world, the path λ2 describing two particle exchanges is continuously deformable to λ1 by taking it behind or front of the right-most particle, and in turn λ1 is contractible to a point. Hence, all the paths have the same topology and thus correspond to the same statistical quantum evolution.

In 2-dimensionnal world, however, the paths λ2 and λ1 are not topologically equivalent since λ2 can not be deformed through the right-most particle, while λ1 is still contractible to a point. Hence, the paths now have different topology and different statistical quantum evolutions can be assigned to each.

This means that , in a 2-dimensional world, particle statistics are different than statistics in higher dimensios. Indeed, quasiparticles can be observed that obey statistics ranging continuously between Fermi–Dirac and Bose–Einstein statistics. In the case of two particles this can be expressed as

$|\psi_1 \psi_2\rangle = e^{i\varphi} |\psi_2 \psi_1\rangle$

Obviously:

For $\varphi= \pi$ , we recover the Fermi–Dirac statistics (since $e^{i \pi} = -1$ ) and,
For $\varphi= 0$ (or $\varphi= 2\pi$ ), we recover the Bose–Einstein statistics (since $e^{i 2\pi} = 1$ ).

In between these cases, we have something completely different. Nobel prize Frank Wilczek coined the term “anyon” to describe such quasiparticles, since they can have any phase when particles are interchanged.

Anyons are somehow neither fermions nor bosons. Like fermions, they cannot occupy the same state. Thus, the world lines of two anyons cannot intersect or merge, which allows their paths to form – you guessed it – braids in space-time:

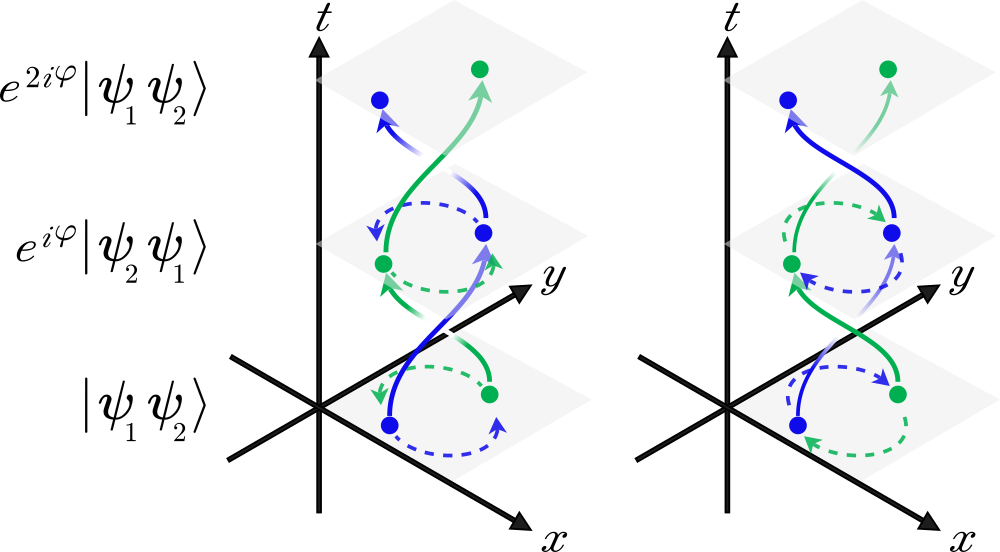
Anyons are best described by a braid group. They are generally classified as abelian or non-abelian. Non-abelian means the order of the rotations matters: swapping anyons A and B and then B and C, for example, produces different braids than swapping B and C then A and B. This distinction enables the particles to serve as qubits because their states will uniquely depend on how they have been braided around each other, encoding the steps of a quantum algorithm. For non-Abelian anyons, the process of braiding can be equivalent to multiplication by an unitary matrix.

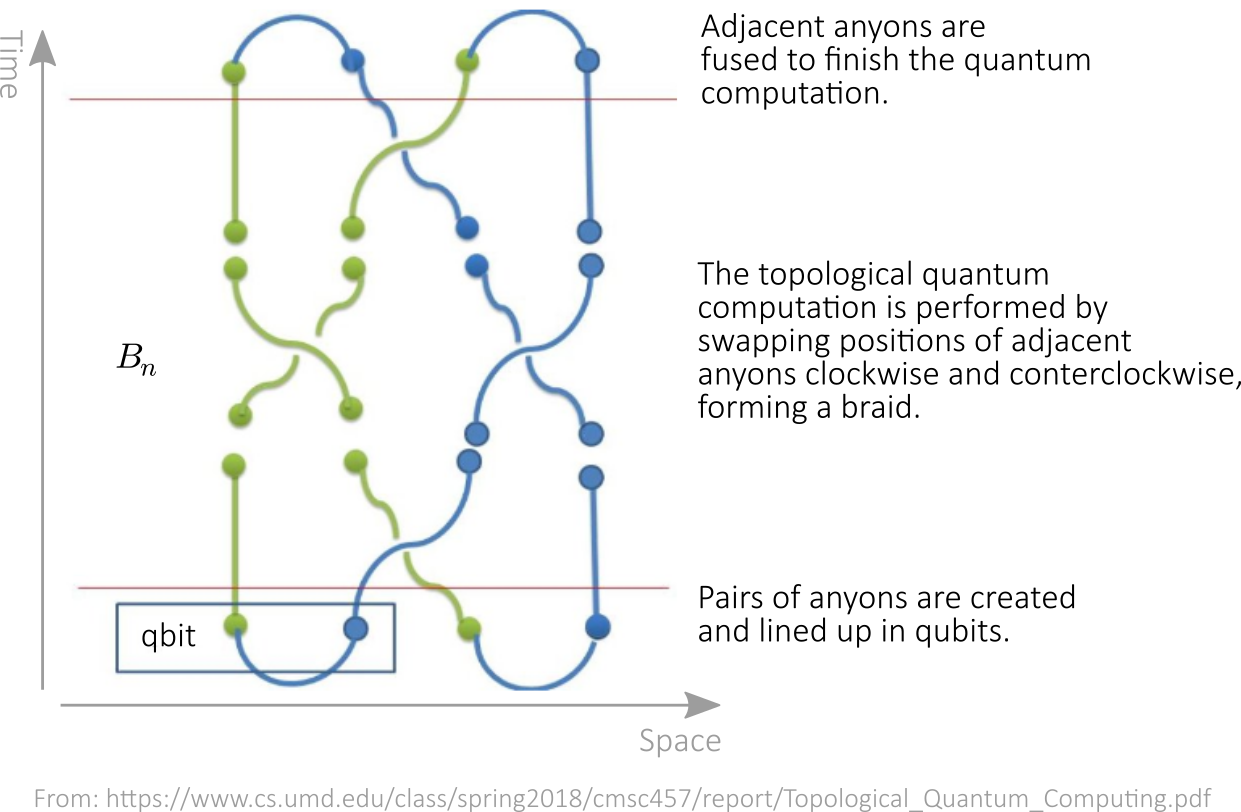
Crucially, just as touching knotted shoelaces won’t untie them, random environmental perturbations won’t unravel the braids of topological qubits. If non-abelian anyons exist and can be braided, they can theoretically form the building blocks of a robust, scalable quantum computer. The unitary gate operations are carried out by braiding quasi-particles, and then measuring the multi-quasi-particle states.

Topological quantum computer

We introduced topology earlier on, with the commonly used example of the topological equivalence between a donut and a coffee cup – regardless of the local details that give them rather different everyday practicalities. Small smooth deformations, such as taking a bite on the side of the donut or chipping away a piece of the cup will change the object locally, but the topology remains unchanged. Only global violent deformations, such as cutting the donut in half or breaking the cup handle, will change the topology by removing the hole.

However, in the quantum world, small deformations matter. To store a quantum state coherently, one must take exceptional care that no outside noise interferes and that the evolution is precisely the desired one. This is the fundamental challenge for practical quantum computation: robustly store quantum states for long times and let them evolve according to specific quantum gates.

Here comes Alexei Kitaev’s idea : were quantum information encoded in topological properties of matter, and were the quantum gates dependent only on the topology of the evolutions, then both should be inherently protected from local perturbations. Such topological quantum computation would exhibit inherent hardware-level stability that ideally would make elaborate schemes of quantum error correction redundant.

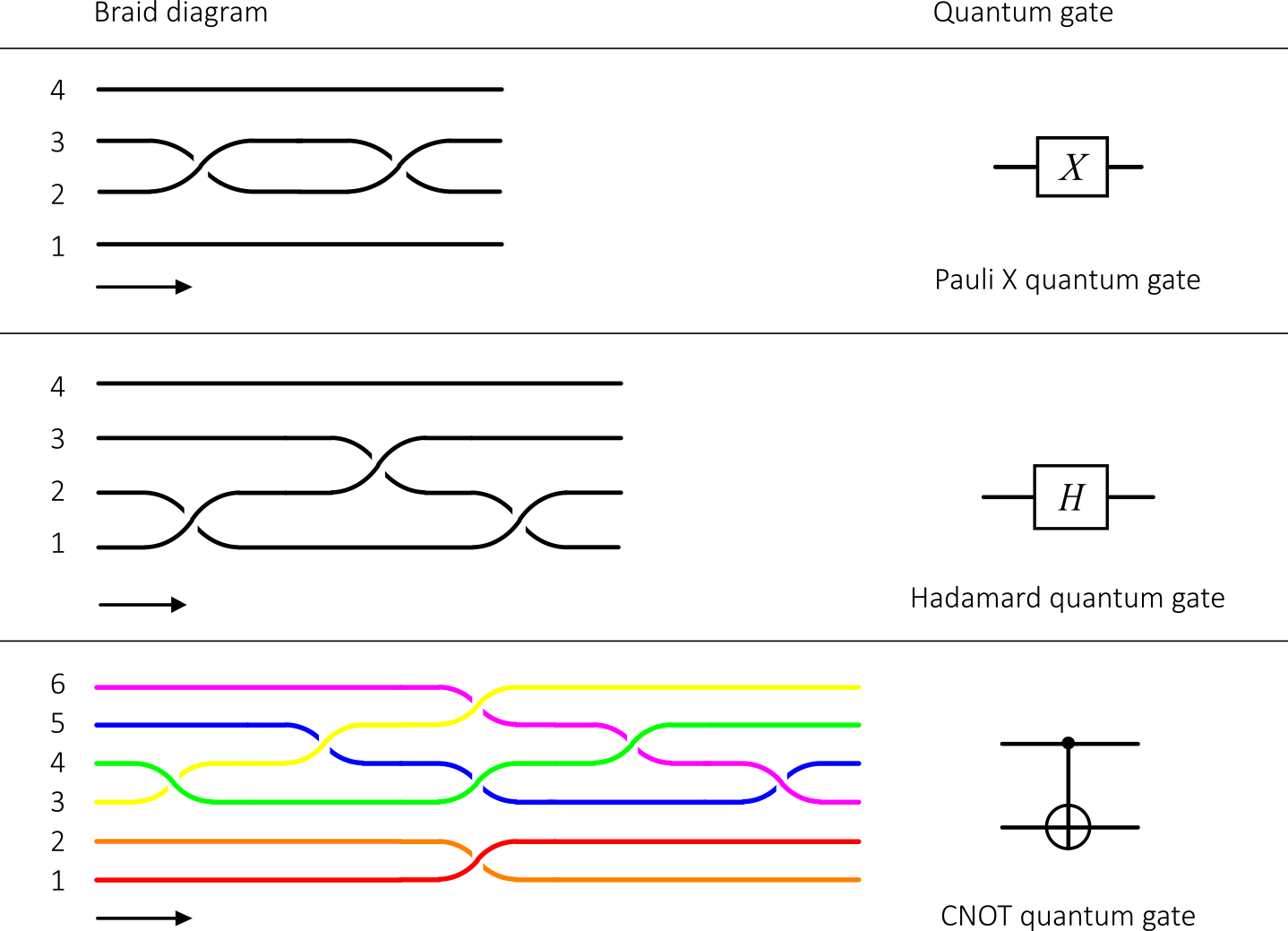
In order to describe how to carry out a quantum computation, one has to initialize a state (create pairs of anyons), perform a quantum gate (braiding), and they finally measure the outcome:

These are braid diagrams and their corresponding quantum gates (see “Topological Quantum Computation with non-Abelian anyons in fractional quantum Hall states“):

Experimentation

Nowadays it is impossible to talk of distinct phases of matter without talking about topology. Without going into the details, mathematically every topological state of matter is characterized by some topological invariant: topological insulators, superconductors, Weyl or Dirac semi-metals, integer and fractional quantum Hall effect or spin liquids are all instances of topological states of matter.

Experimental evidence of non-abelian anyons are not yet fully conclusive. There are many experimental challenges to be met before a topological qubit sees the light. But everyone agrees that the concept of topological quantum computation is so attractive that it is worth a try.

Majorana particles, hypothesized by the great Ettore Majorana in 1937, is a fermion that is its own antiparticle. In superconducting materials, Majorana fermions can emerge as quasiparticles (known as Bogoliubov quasiparticles in condensed matter). This becomes possible because a quasiparticle in a superconductor is its own antiparticle: Majorana bound states are an example of non-abelian anyons. Bound Majorana particles behave as quasiparticles when in solid state and, more important, are exactly of the kind of two-dimensional quasiparticles required by topological quantum computers.

In April 2018, a joint team of researchers (Microsoft Research, Technical University of Delft, …) lead by Hao Zhang (above picture) and Leo Kouwenhoven successfully detected, for the first time, the full effect predicted by theory. The experiment also included variations in some parameters, such as the magnetic field, in order to verify that the signal was indeed the expected for a Majorana particle.

The detection of the Majorana particle could pave the way for new experiments that could soon lead to a topological quantum computer.

Edit (02/15/2021, from Wired “Microsoft’s Big Win in Quantum Computing Was an ‘Error’ After All”): unfortunately, Kouwenhoven and his coauthors released a new paper including more data from their experiments. It concludes that they did not find the prized particle after all. An attached note from the authors said the original paper, in the prestigious journal Nature, would be retracted, citing “technical errors.”

Note: A few paragraphs and illustrations of this post are based on wikipedia’s entries and animations on topology and braid theory.

Leave a Reply Cancel reply