On quantum computing and cryptography

Cryptography is the cornerstone of secure communication. Broadly speaking, cryptography deals with creating and studying protocols that prevent third parties (public or adversaries) from reading messages. It is strongly tied to information security topics such as confidentiality, data integrity, identification, authentication or non-repudiation / proof.

Today’s cryptography is heavily based on mathematics: cryptographic algorithms are designed from computational hardness assumptions. These are asymmetrical problems, like integer factorization: multiplying two integers is easy, factoring a 500-digit integer is not. An introduction to complexity was published in a previous post.

Unconditionally secure schemes (like the he one-time pad) do exist. But these schemes are practically more difficult to implement than the best computationally secure ones.

The idea of “computationally secure scheme” is the following: although it is theoretically possible to break such a system, it is practicality impossible to do so. The balance is easy to understand: if breaking a system costs more that the value it defends, it is worthless to do so.

Both theoretical and practical advances require computationally secure schemes to be continually evaluated and adapted.

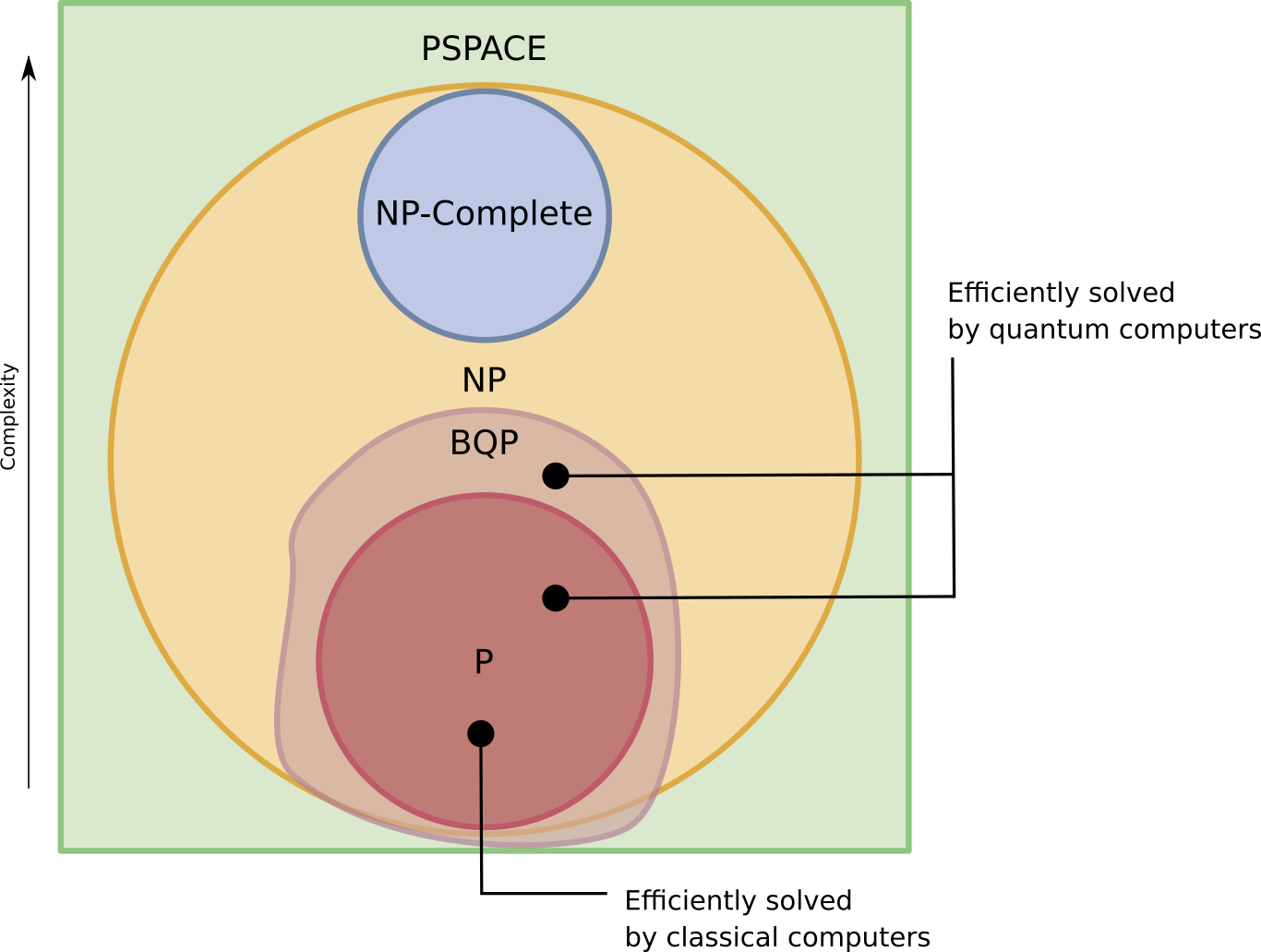
As such, quantum computing poses a threat to encryption schemes based on assumptions about problems that are hard to solve with classical computing (NP complexity class) but happen to be efficiently solved by quantum computers (BQP complexity class):

This is why cryptography enters the quantum realm:

for building (classical) encryption schemes that are considered to be secure against attacks by quantum computers.
for building innovating quantum security schemes (based on quantum properties such as entanglement, no-cloning theorem, …);

First, let’s define our vocabulary:

plaintext: unencrypted text (also called cleartext). Plaintexts will be denoted by the letter $M$ (message);
ciphertext: encrypted text (also called cryptogram). Ciphertexts will be denoted by the letter $C$ ;
encryption: process of transforming plaintext into ciphertext, $C = f(M)$ (where $f$ is an encryption function);
decryption: process of transforming ciphertext into plaintext, $M = f^{-1}(C)$ (where $f^{-1}$ is a decryption function);
cryptographic key: a parameter that determines the output of a cryptographic algorithm. Keys will be denoted by the letter $k$ . For example, for an encryption algorithm, a key specifies the transformation of plaintext into ciphertext: $C = f(M,k)$ ;
hashing: a mathematical function that can be used to map data of arbitrary size to data of fixed size. It is used to verify data integrity.
cryptosystem: a suite of cryptographic algorithms needed to implement a particular security service. A typical cryptosystem consists of three algorithms: one for key generation, one for encryption, and one for decryption.

Now, let’s define our participants:

Alice and Bob: Alice and Bob are fictional characters commonly used as placeholder names in cryptology. They ware were invented by Ron Rivest, Adi Shamir, and Leonard Adleman in their 1978 seminal paper “A method for obtaining digital signatures and public-key cryptosystems.”. These names are used for convenience and to aid comprehension: “How can Bob send a private message $M$ to Alice ?”.
Additional characters can be added as generic participants, like Carol, Dave, …

And finally, let’s define our adversaries:

Eve: Eve is an eavesdropper, who is usually a passive attacker: while she can listen in on messages between Alice and Bob, she cannot modify them;
Mallory and Trudy: Mallory is a malicious attacker, often associated with Trudy, the intruder. Mallory and Trudy are active attackers (often used in man-in-the-middle attacks), who can modify messages, substitute messages, or replay old messages.

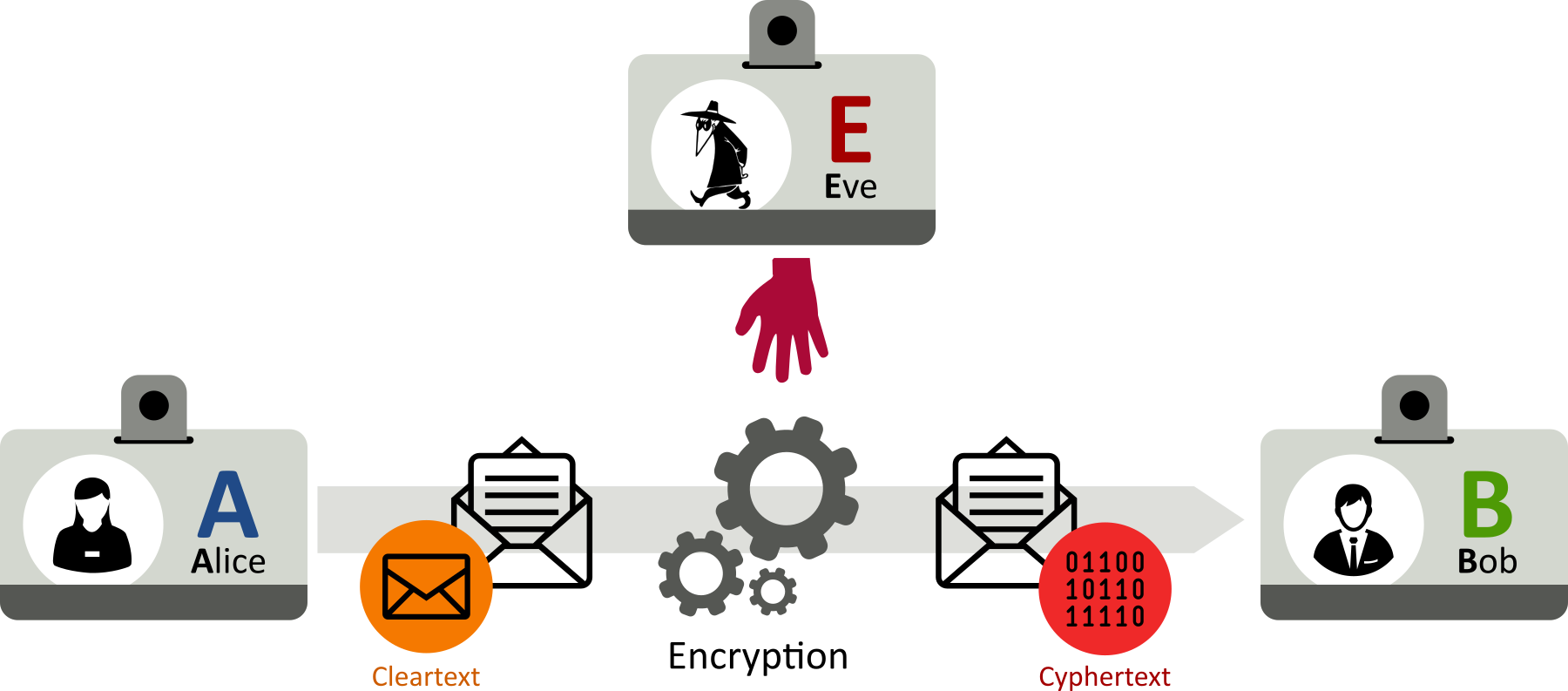
There are many other characters: Wendy (the whistleblower, an insider with privileged access capable of divulging information), Olivia (the oracle, who, for example, provides external data to smart contracts residing on distributed ledger systems), or Arthur and Merlin (usually appearing in interactive proof systems: Merlin – who has unbounded computational abilities – claims the truth of a statement, and Arthur questions him to verify the claim), …

Now that the vocabulary is settled, let’s explore common classical (i.e. non-quantum) cryptography.

Symmetric-key algorithm (classical)

Symmetric-key algorithms use the same cryptographic keys for both encryption of plaintext and decryption of ciphertext:

$C = f(M,\mathbf{k})$
$M = f^{-1}(C,\mathbf{k})$

This key, in practice, is a shared secret between the parties, used to keep the communication link private.

The first symmetric-key algorithms historically appeared very early (ancient Greece’s Scytale, Caesar shift, …). To encrypt cleartext messages, simple algorithms were used, using transpositions or mono-alphabetical substitutions.

In the case of Caesar shift, each letter in the plaintext is shifted, replaced by a letter some fixed-number of positions down the alphabet:

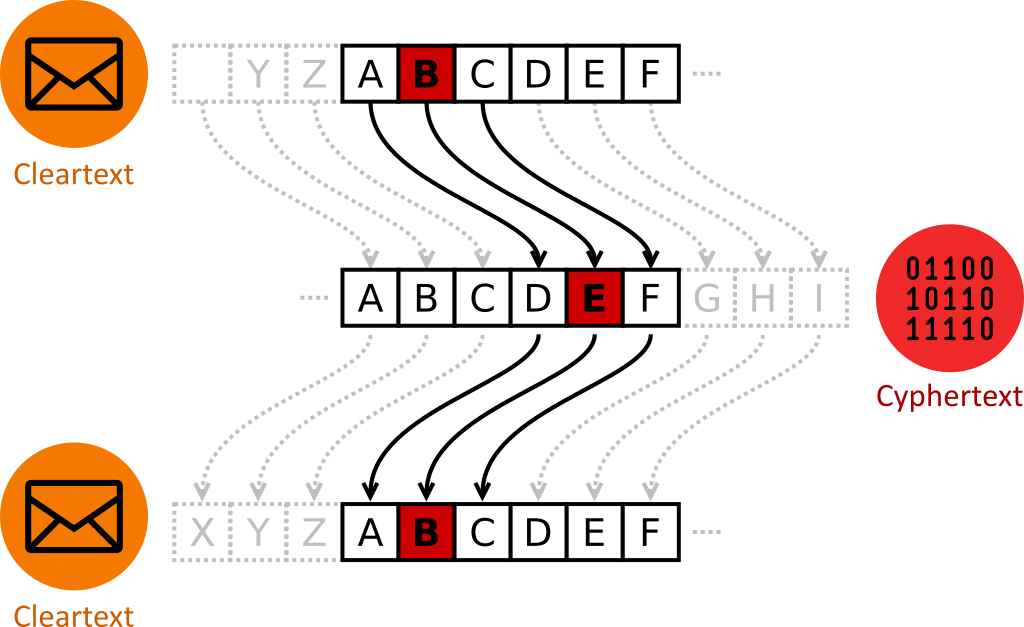
In this scheme, the encryption key is the shift. It is a secret that has to be shared through a separate secure channel. Knowing the key, one can encrypt and decrypt messages.

Though very simple and ancient, it holds nice properties:

It’s strength doesn’t rely on the secrecy of algorithm (which is known), but relies on the secrecy of the key (which is easier to change than the algorithm)
Since the algorithm is known, it can be studied. Once considered too weak (or broken), it shall be replaced by a more efficient one, which also will be studied, and so on …

These are actually modern qualities, as defined by the Kerckhoffs’s principle: “A cryptosystem should be secure even if everything about the system, except the key, is public knowledge“, or, as formulated by Claude Shannon: “One ought to design systems under the assumption that the enemy will immediately gain full familiarity with them”. Or in even simpler terms: security by obscurity doesn’t work, never worked and will never work.

Of course, Caesar shift is easy to break, using simple techniques such as frequency analysis.

Jumping forward in time (around 1590), new algorithms were proposed, using polyalphabetic substitutions techniques for example. The famous Vigenère cipher is one of them:

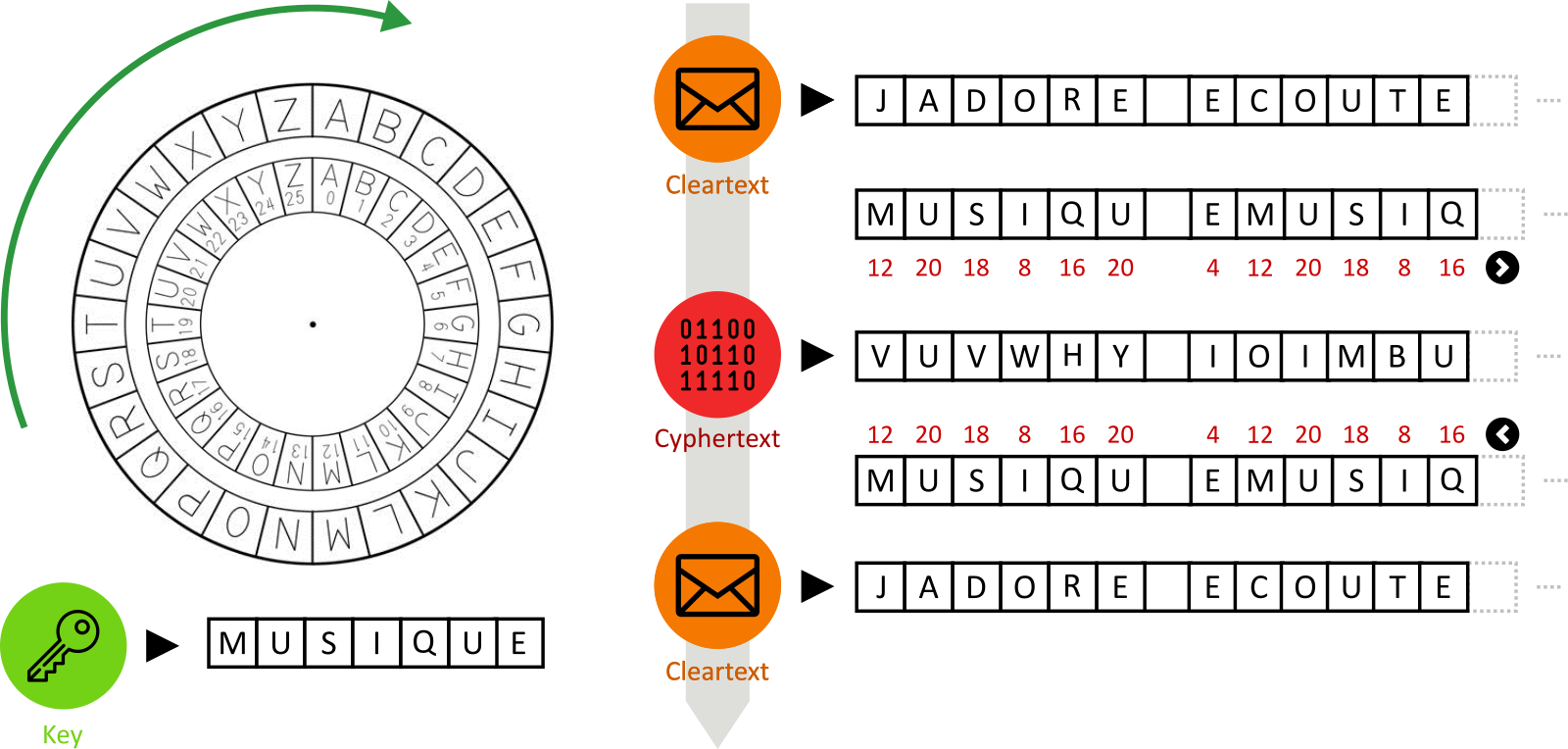
Here, the encryption key is “MUSIQUE” (french for “music”) and is used to encrypt “JADORE ECOUTER…” (which is french for “I like to listen…”).

This cipher gained a reputation for being exceptionally strong. It stood its ground until the early 1900’s, where is was finally broken.

Gilbert Vernam tried to repair the broken cipher, but, no matter what he did, the cipher was still vulnerable to cryptanalysis. Vernam’s work, however, eventually led to the one-time pad, a theoretically unbreakable cipher !

The one-time pad algorithm it rather simple. It applies XOR operations on pairs of cleartexts and keys, given the following requirements:

keys are perfectly random;
the set of keys is secret (and previously shared through a secure channel);
each key is at least as long as the current cleartext;
each key is never reused, in whole or in part (hence the term one-time pad)

One-time pads are “information-theoretically secure” (sometimes also called “perfect secrecy”). This is a very strong notion of security, developed by Claude Shannon. He also mathematically proved that, with the previous requirements, one-time pads are secure even against adversaries with infinite computational power.

But, alas (!), despite Shannon’s proof of its security, one-time pad have serious practical drawbacks :

Truly random (as opposed to pseudorandom) one-time pad values, which is a highly non-trivial requirement.
Secure generation and exchange of the one-time pad values, which must be at least as long as the message: the security of the one-time pad is only as secure as the security of the one-time pad exchange !
Making sure that keys continues to remain secret, and are disposed of correctly, preventing any reuse in whole or part. See for data remanence to get an idea of practical difficulties in completely erasing computer media…

Unfortunately, this means that one-time pads solve only few current practical problems: we have to rely on other high quality ciphers, which are widely available, but are not unconditionally secure schemes.

Today’s golden standard for symmetric-key algorithm is the Advanced Encryption Standard (AES, a.k.a Rijndael). It has been adopted by the U.S. government and is now used worldwide (FIPS PUB 197, ISO/IEC 18033-3). It supersedes the Data Encryption Standard (DES) encryption scheme, which is now considered outdated (weak).

AES is based on a substitution–permutation network (rounds of substitutions and permutations):

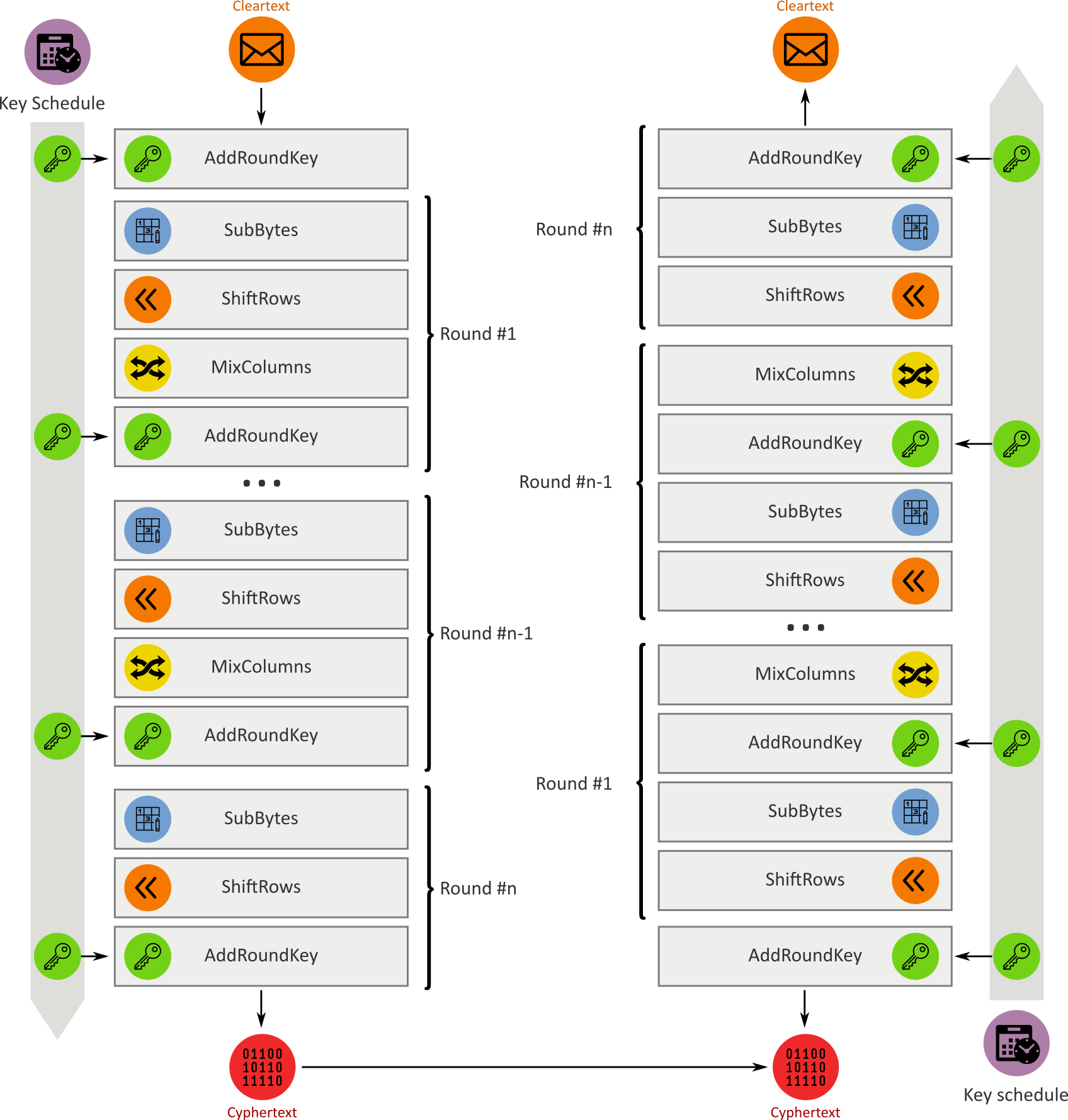
Round keys are derived from the secret key using Rijndael’s key schedule.

At the time of writing, there is no known practical attack that would allow someone without knowledge of the key to read data encrypted by AES when correctly implemented.

Nevertheless, symmetric-key requirement that both parties have access to the secret key is one of the main drawbacks of symmetric-key encryption, in comparison to public-key encryption, that we will now discuss.

Asymmetric public-key algorithm (classical)

The idea of an asymmetric public-private key cryptosystem is attributed to Whitfield Diffie and Martin Hellman. These are cryptographic system that uses pairs of keys:

public keys which may be distributed publicly;
private keys which are known only to the owner (and thus shall be protected accordingly);
What is encrypted with a public key can only be decrypted by the associated private key;
Conversely, what is encrypted with a private key can only be decrypted by the associated public key.

With these requirement, in a public key encryption scheme:

Any person can encrypt a message using the receiver’s public key and that encrypted message can only be decrypted with the receiver’s private key;
The strength of a public key cryptography system relies on the computational effort required to find the private key from its associated public key. Effective security only requires keeping the private key private: the public key can be openly distributed without compromising security.

The first step towards public-key encryption is thus the creation of pairs of keys with these properties. Each party (Alice and Bob) generates two keys:

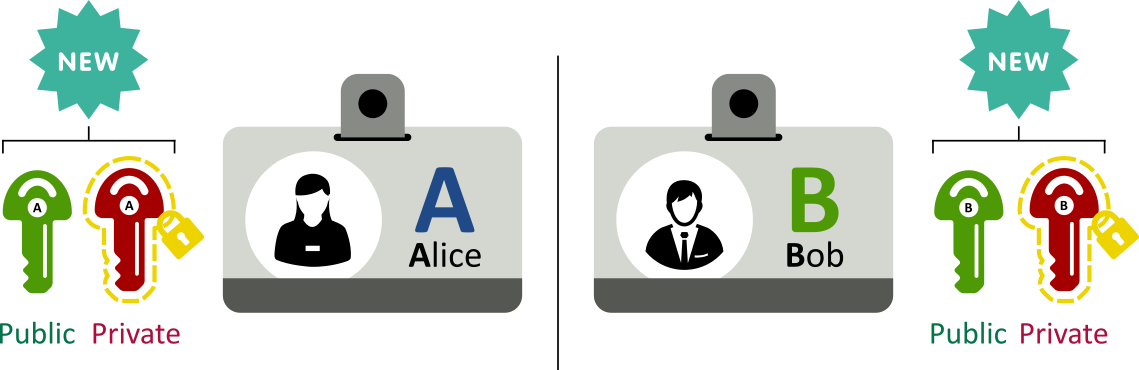
The private keys are to be kept secured ! Usually, they are encrypted using a symmetric-key algorithm, protected by a passphrase only known to its owner.

The next step is the exchange of the public keys between parties (Alice and Bob):

Please, note that:

public-key algorithms schemes, unlike symmetric-key ones, do not require a secure channel for the initial exchange of one or more secret keys between the parties;
formally associating public keys with the identity of their owners (i.e. key certification, which is not required for encryption) necessitates additional steps, protocols and components (third party authorities, webs of trust, distributed ledgers, …).

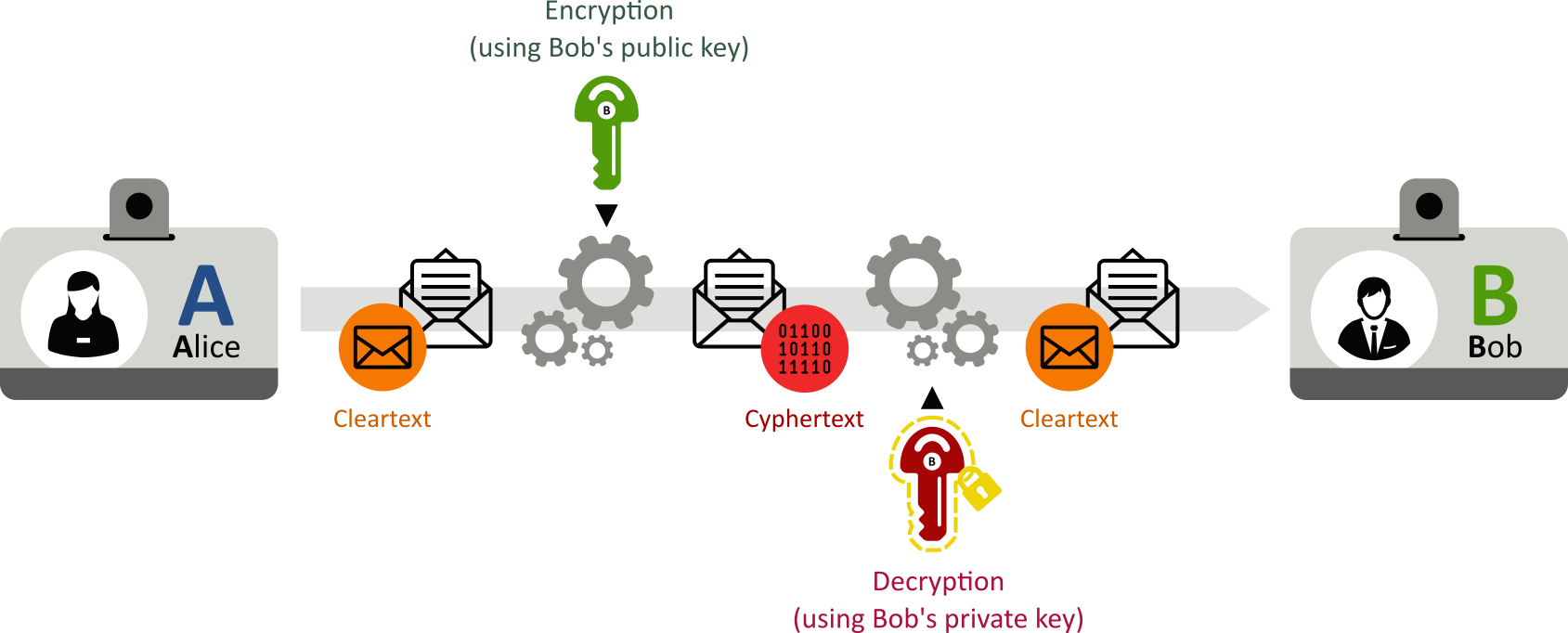
Once public keys are distributed, they can be used to encrypt messages. If Alice wants to send a message that can only be read by Bob:

Alice encrypts his message with Bob’s public key: $C = f\big(M,k_{pub}(\mathsf{Bob})\big)$ ;
Bob decrypts the message with his private key: $M = f^{-1}\big(C,k_{priv}(\mathsf{Bob})\big)$ ;
Since he is the (only) holder of his private key, Bob is the only one able to read Alice’s message (unless Trudy stole Bob’s private key…).

Conversely, public-key schemes can be used for authentication. Here, the public key is used to verify that a holder of the paired private key sent the message:

Alice encrypts his message with his private key: $C = f\big(M,k_{priv}(\mathsf{Alice})\big)$ ;
Anyone can decrypt Alice’s message (since Alice’s public key is available to anybody): $M = f^{-1}\big(C,k_{pub}(\mathsf{Alice})\big)$
Since she is the (only) holder of her private key, Alice is the only one that could have encrypted the message.

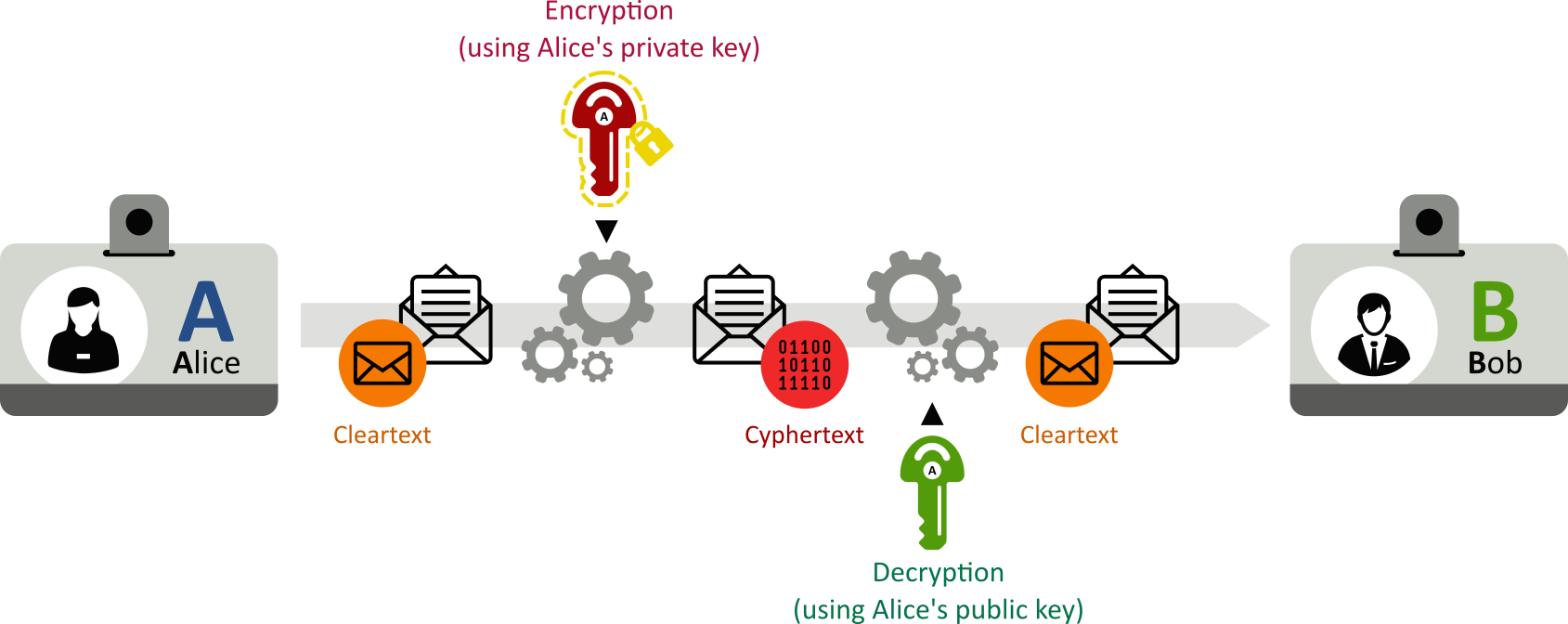
Please, note that Alice was not actually authenticated: only here (private) key was. Some kind of certification would have be required to actually authenticate Alice.

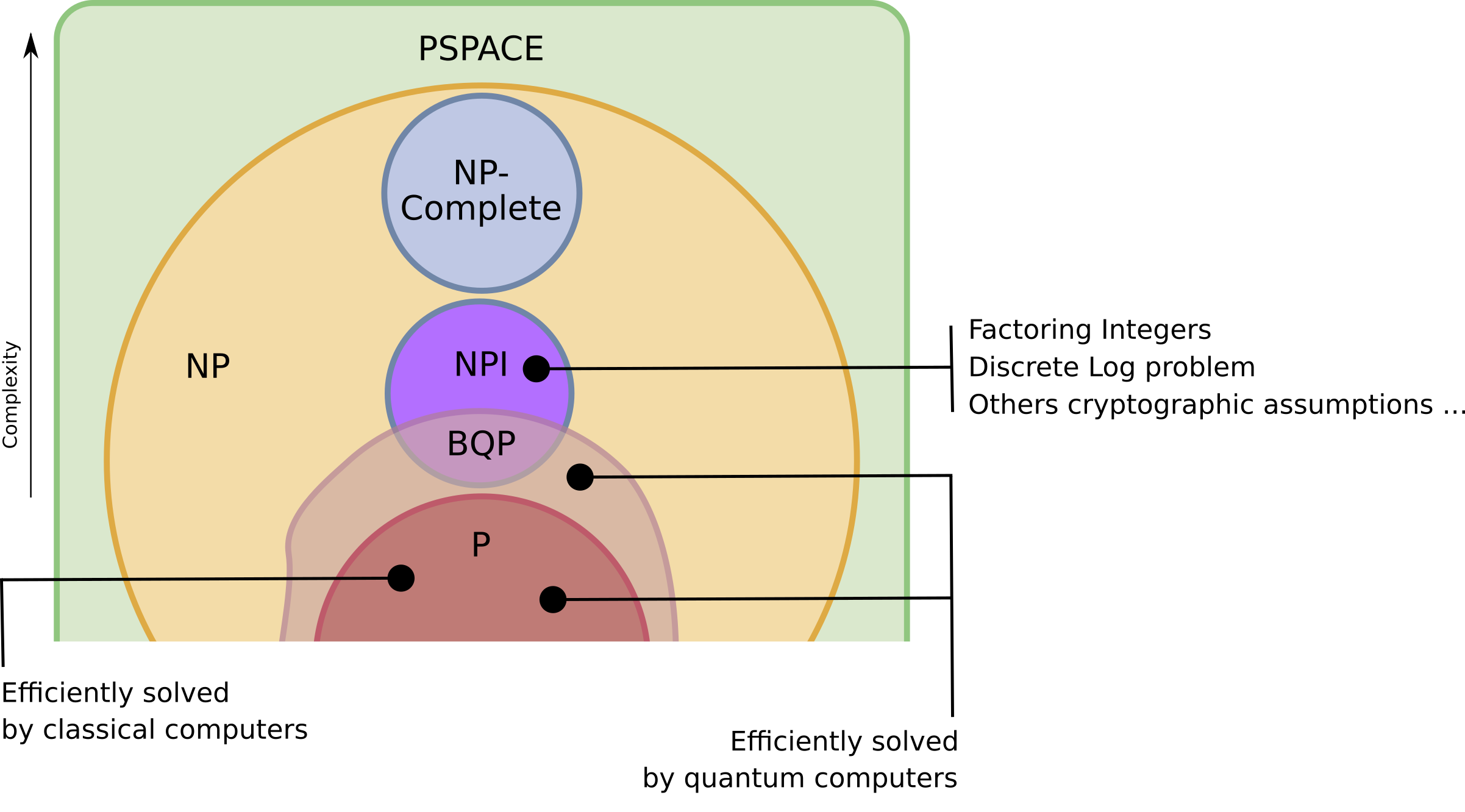
Public key cryptography algorithms are mostly based on hard mathematical problems without (classical) efficient solution : integer factorization, discrete logarithm, and elliptic curve relationships, …

Usually, these problems are thought to be of NP-intermediate (NPI) class: problems in the complexity class NP but that are neither P nor NP-complete. This idea is crudely (especially the NPI / BQP intersection) sketched in the following diagram:

Let’s focus a moment on the RSA cryptosystem, one of the most widely used public-key cryptosystems. RSA is an acronym based on the surnames of Ron Rivest, Adi Shamir, and Leonard Adleman.

It is based on the following modular arithmetic observations:

it is easy to find three very large positive integers $e, d$ and $n$ such that $\forall m \in \mathsf{Z}$ with $0 \leq m < n\$ : $(m^e)^d \equiv m\ (\mathrm{mod}\ n)$ – or, conversely, that $(m^d)^e \equiv m\ (\mathrm{mod}\ n)$ ;
$e$ .

Proof of these observations can be obtained either via Fermat’s little theorem (in RSA’s original paper) or via Euler’s theorem (proof easier to derive).

In this scheme, the public key is represented by ${e,n}$ , the private key is represented by ${d,n}$ and the integer $m$ represents the message.

RSA keys are generated the following way:

Randomly choose two prime numbers $p$ and $q$ ;
Calculate the modulus $n = p \times q$ ;
Calculate Euler’s totient function: $\varphi(n) = (p-1) \times (q-1)$ ;
Choose $e$ so that $\mathrm{gcd}(e,\varphi(n))=1$ and $e > \varphi(n)$ ;
Calculate $d \equiv e^{-1}\ (\mathrm{mod}\ \varphi(n))$ ;
$k_{pub} = \{e,n\}$
$k_{priv} = \{d,n\}$

They are used as follows:

encryption: $C = f(M,k_{pub}) \equiv M^e\ (\mathrm{mod}\ n)$
decryption: $M = f^{-1}(C,k_{priv}) \equiv C^d\ (\mathrm{mod}\ n)$

To calculate $k_{priv}=\{e,n\}$ from $k_{priv} = \{d,n\}$ , one has to know $\varphi(n)$ . Hence, to calculate $k_{priv}=\{e,n\}$ from $k_{priv} = \{d,n\}$ one has to know $p$ and $q$ : RSA’s strength resides in the hardness of prime factoring $n$ .

The problem is clearly in class NP, but has not been proved to be or not be NP-complete. No prime decomposition classical algorithm has been published that can factor all integers in polynomial time. We will however see that this is a completely different story for quantum algorithms).

Public key algorithms are fundamental security ingredients :

they underpin various Internet standards, such as Transport Layer Security (TLS) or S/MIME;
some public key algorithms provide key distribution and secrecy (e.g., Diffie–Hellman key exchange).

Combined with hashes (that will be discussed in the next paragraph), public key cryptography:

provides digital signatures;
provides methods for assuring and non-repudiability.

Cryptographic hash functions (classical)

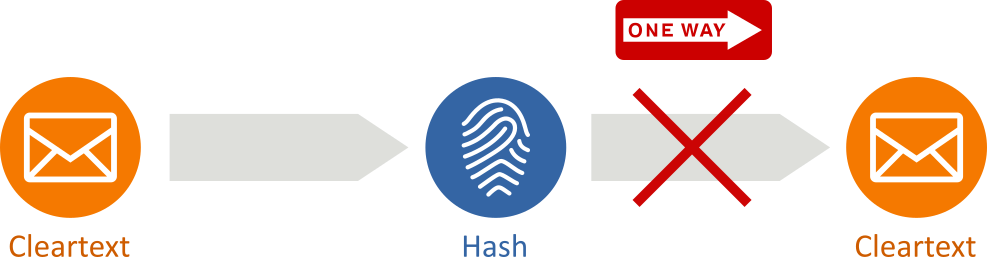
Cryptographic hash functions are a special class of hash function (see definition at the beginning of this post) that has certain properties – other than being easy to compute – which make them suitable for use in cryptography:

They are designed to be a one-way function, that is, a function which is infeasible to invert:

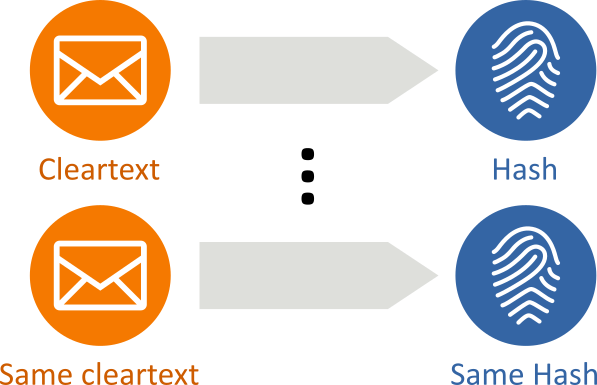
They are deterministic: the same message always results in the same hash:

A small change to a message should change the hash value so extensively that the new hash value appears uncorrelated with the old hash value (quick divergence):

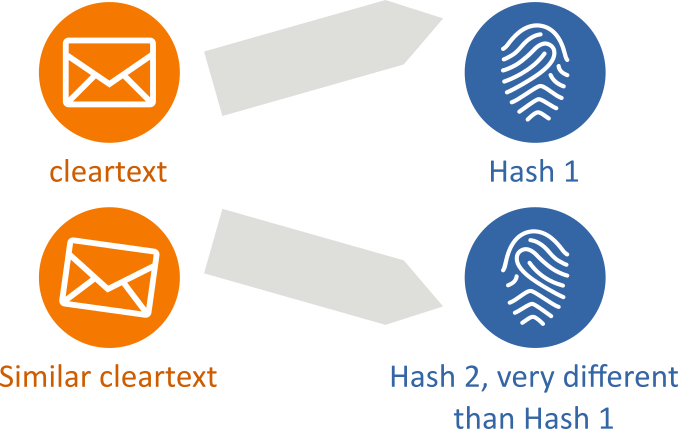
It is infeasible to find two different messages with the same hash value (no collisions):

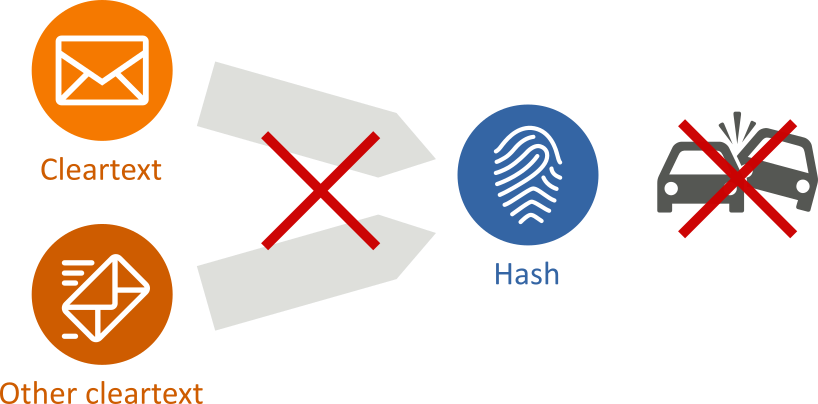
Cryptographic hash functions are widely used as they have many security applications, such as:

fingerprinting (for data deduplication purposes for example);
verifying the integrity of files or messages;
password verification;
proof of work in blockchain technologies;
digital signatures;
message authentication codes (MACs);
file or data identifier;
pseudorandom generation and key derivation;
…

Cryptographic hash functions can be build using the Merkle–Damgård construction:

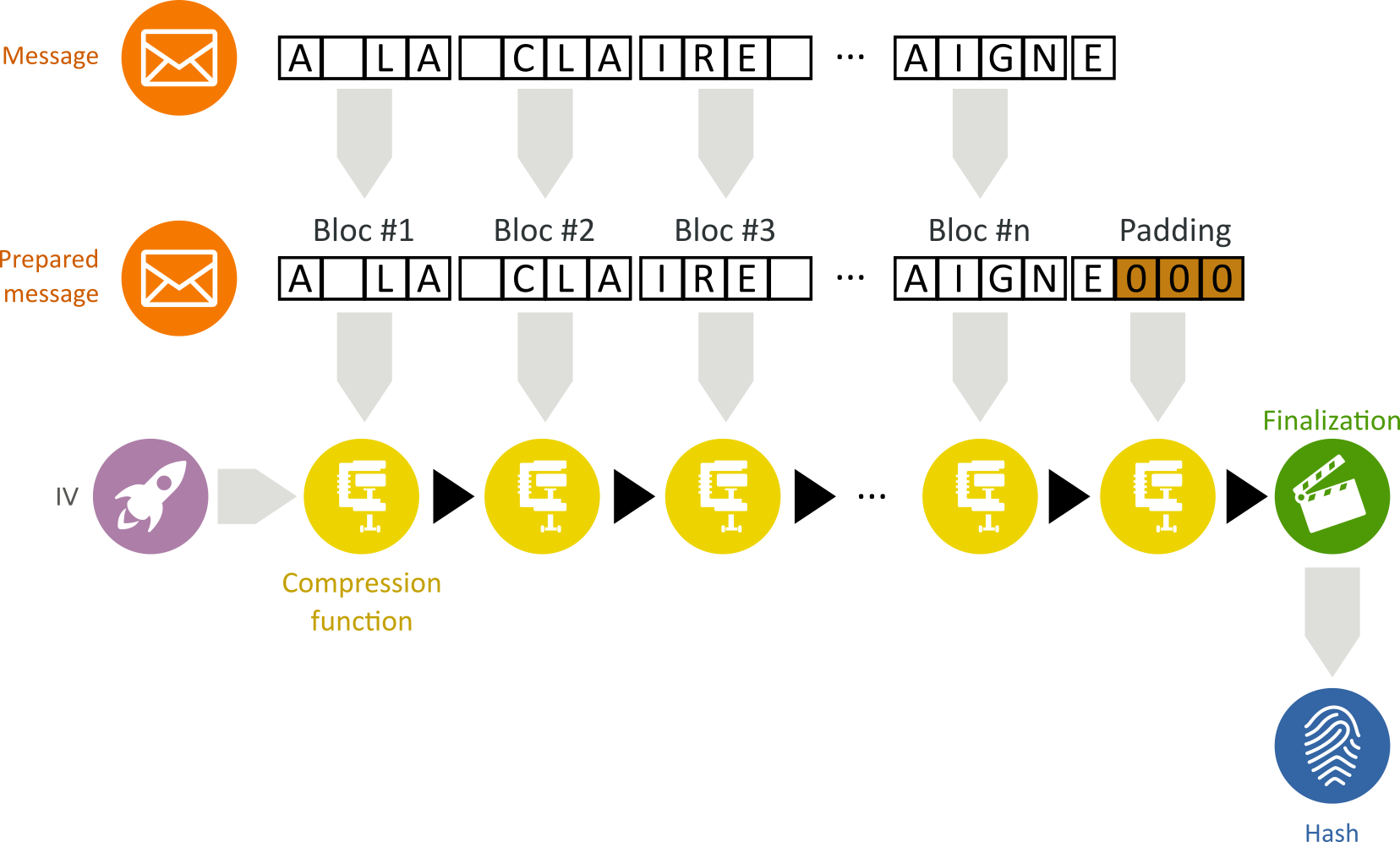
The input message (here, an extract from a french song “A la claire fontaine, m’en allant promener, j’ai trouvé l’eau si belle que je m’y suis baigné”) is broken into a series of equal-sized blocks to form a prepared message;
A initialization vector (IV) is introduced;
For each message block, the compression function takes the result so far (using the IV as initial value), combines it with the message block, and produces an intermediate result;
The last block is padded with zeros as needed;
To harden the hash further, the last result is then fed through a finalization function.

Common classical hash functions, including SHA-1, SHA-2 or MD5 are based on the Merkle–Damgård construction. Just like any other cryptographic algorithms, hash functions have to be studied, put to the test and have to be discarded when proven to be not enough effective.

Indeed, both SHA-1 and MD5 are severely compromised as they are both vulnerable to collision attacks: SHA-1 and MD5 shall not be used anymore.

Similarly, SHA-256 and SHA-512 are prone to length extension attacks, rendering them insecure for some applications.

The SHA-3 cryptographic hash function is based on a different scheme, called the sponge construction:

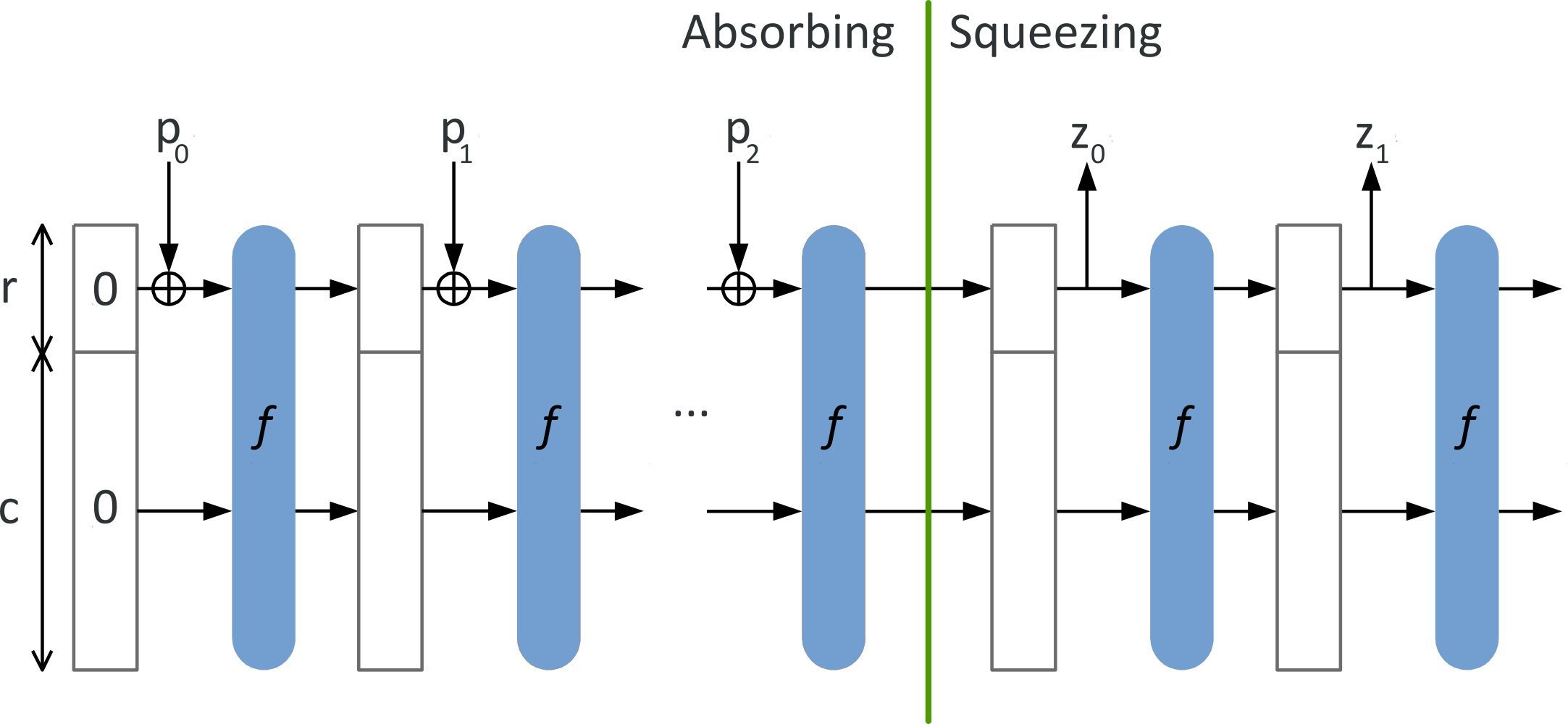
In this construction, data is “absorbed” into the sponge, then the result is “squeezed” out:

in the absorbing phase, message blocks are XORed into a subset of the state, which is then transformed as a whole using a permutation function.
in the “squeeze” phase, output blocks are read from the same subset of the state, alternated with a state transformation function.

The purpose of SHA-3 is that it can be directly substituted for SHA-2 in current applications if necessary.

Key distribution (classical)

As we have seen, for symmetric key cryptography, both parties must share a common secret key before using any encryption.

Alas, distribution of secret keys has always been problematic. Traditionally, secure communication between two parties required that they first exchange keys by some secure physical channel: face-to-face meeting, use of a trusted courier …

Diffie–Hellman key exchange (DH) is a way of generating a shared secret between two people in such a way that the secret can’t be seen by observing the communication.

DH is non-authenticated key-agreement protocol which allows two parties that have no prior knowledge of each other to jointly establish a shared secret key over an insecure channel. There is an important distinction here: parties are not sharing information during the key exchange, parties are creating a key together. This key can then be used to encrypt subsequent communications using a symmetric key cipher.

This is particularly useful because you can use this technique to create an encryption key with someone, and then start encrypting your traffic with that key.

DH essentially breaks down to following steps:

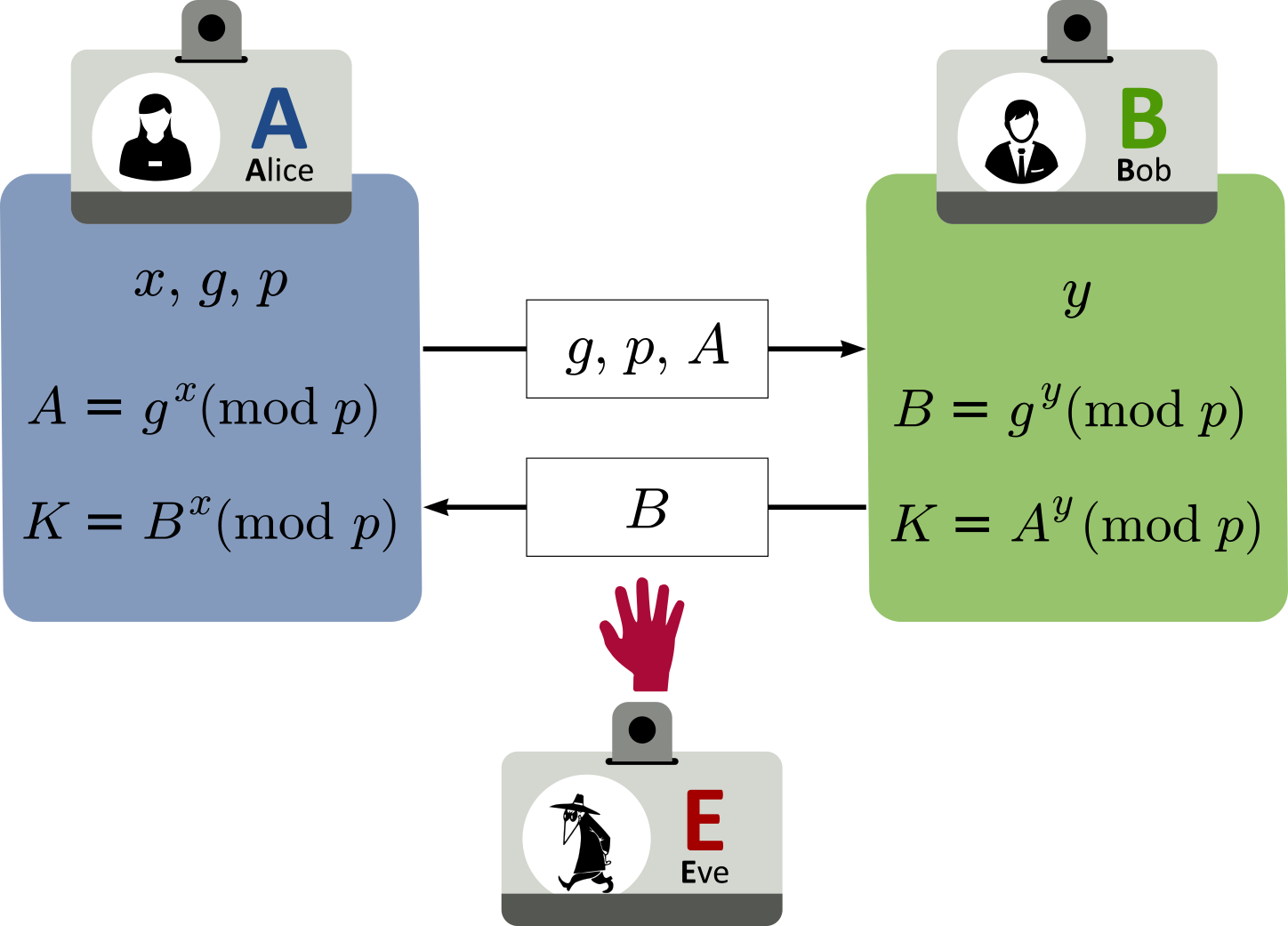
Each party agrees on a public value $g$ and a large prime number $p$ ;
Next, one party chooses a secret value $x$ and the other party chooses a secret value $y$ ;
Both parties use their secret values to derive public values: $g^x (\mathrm{mod}\ p)$ and $g^y (\mathrm{mod}\ p)$ ;
Alice and Bob exchange these public values. Each party then uses the other party’s public value to calculate the shared secret key that is used by both parties for confidential communication;
Alice uses the value $g^{xy} (\mathrm{mod}\ p)$ as her secret key for confidential communications with Bob;
Conversely Bob uses the value $g^{yx} (\mathrm{mod}\ p)$ as his secret key.

Because $g^{xy} (\mathrm{mod}\ p) = g^{yx} (\mathrm{mod}\ p)$ , Alice and Bob can use their secret keys with a symmetric key algorithm to conduct confidential online communications. The use of the modulo function ensures that both parties can calculate the same secret key value, but an eavesdropper cannot.

Variations of the described DH scheme exist. For example, the Elliptic curve Diffie–Hellman (ECDH) protocol is variant that uses elliptic curves instead of the multiplicative group of integers modulo $p$ .

Even if the traffic is recorded and later analyzed, there’s no way to figure out what the key was, even though the exchanges that created it may have been visible (see perfect forward secrecy) because the secret key is known only to each party and was never visible on the network.

If Eve (the eavesdropper) intercepts the values of $g$ and $p$ , because of the hard mathematical problem created by the use of a large prime number in $(\mathrm{mod}\ p)$ , she would not be able to feasibly calculate either secret value $x$ or secret value $y$ : for Eve to resolve the DH (or ECDH) problem, she would have to solve a discrete logarithm problem, which is of NPI complexity and is not solvable for classical computers in polynomial time.

How secure is classical cryptography against quantum computing?

In cryptography, security level is a measure of the strength that a cryptographic primitive (cipher, hash function, …). They are usually expressed in bits, where n-bit security means that the attacker would have to perform $2^n$ operations to break it. Though not perfect, it allows convenient comparison between algorithms. For example, AES-128 (key size 128 bits) is designed to offer a 128-bit security level, which is considered roughly equivalent to 3072-bit RSA.

Let’s start with symmetric-key algorithms. They usually have a strictly defined security claim, typically equal to the key size of the cipher (equivalent to the complexity of a brute-force attack).

Symmetric encryption algorithms are affected by quantum computing: Grover’s Algorithm does provide a significant speed-up by finding the solution in the square-root of the time of a classical computer:

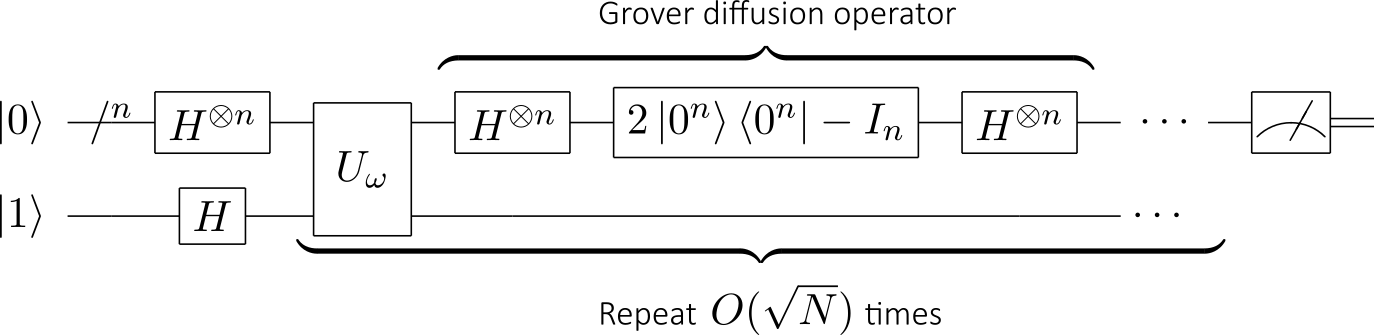
For example, AES-256 has up to 2²⁵⁶keys. A quantum computer could make that same search as if there were only 2¹²⁸ keys. On the one hand, that’s a lot faster. On the other hand, it’s still an awful lot of searching to do…

Algorithm	Key length	Security Level (classical)	Security Level (quantum)
AES-128	128 bits	128 bits	64 bits
AES-256	256 bits	256 bits	128 bits

Therefore, to counteract this quadratic speedup, larger key sizes must be used. AES-like ciphers are usually considered quantum-safe as long as the key length is $\geq$ 256 bits, which is no big deal.

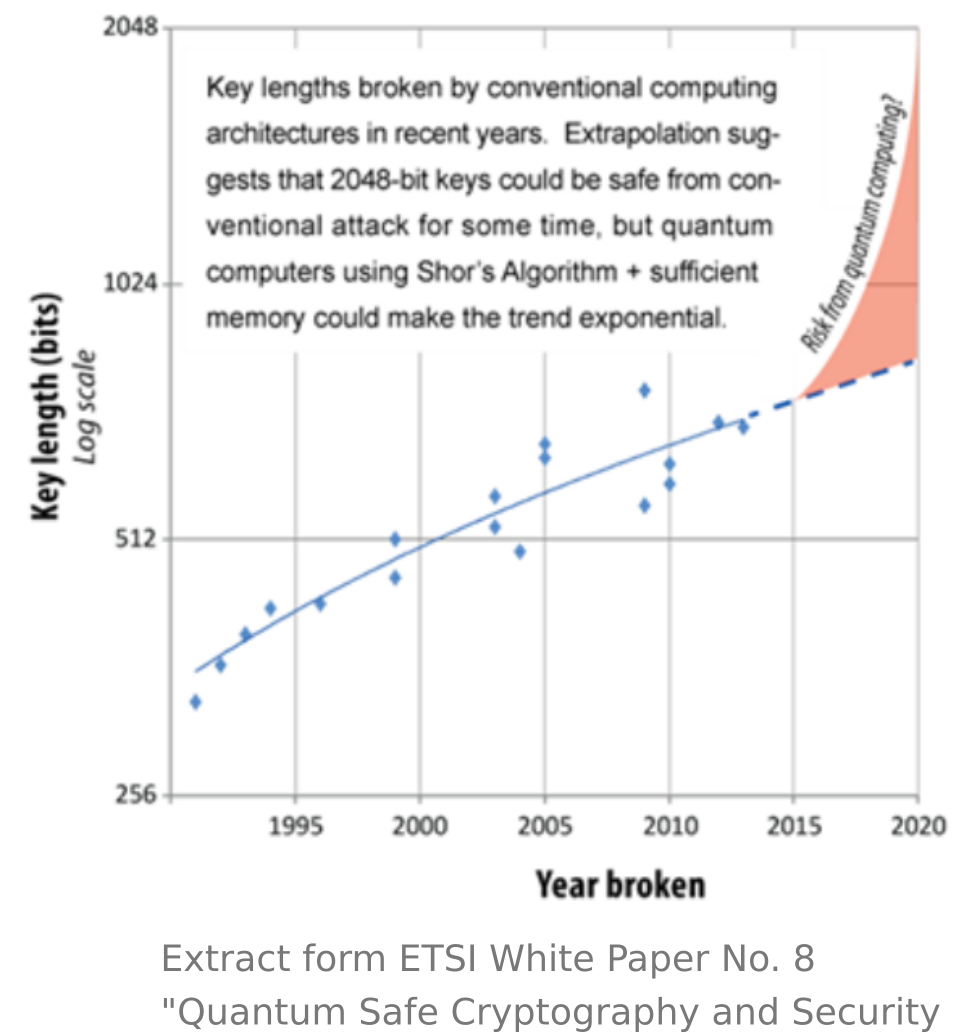
However, it is a completely different story for public-key algorithm. Indeed, we have seen in a previous post that Shor’s algorithm is able to solve prime factoring problems in polynomial time : it takes only $O(b^3)$ time and $O(b)$ space on b-bit number inputs:

It means that, this time, quantum computers are predicted to get exponential speed-up. Therefore, RSA-like and ECC-like (Elliptic Curve) ciphers are not considered quantum safe because they are not able to adapt by increasing their key sizes to outpace the rate of development of quantum computing.

Algorithm	Key length	Security Level (classical)	Security Level (quantum)
RSA-1024	1024 bits	80 bits	0 bits
RSA-2048	2048 bits	112 bits	0 bits
ECC-256	256 bits	128 bits	0 bits
ECC-384	384 bits	256 bits	0 bits

Concerning cryptographic hash function, quantum computers seem to provide some non-trivial quadratic speedup (via the use of the Grover algorithm).

Moreover, for collision resistance, quantum computers provide an even less impressive speed-up: the classical birthday attack gives a $O(\sqrt{n})$ attack, and it’s quantum version seems only to make this attack $O(n^{1/3})$ . It has been proven for example that the Merkle–Damgård construction (as used by SHA-2), is quantum collision-resistant. The sponge construction (as used by SHA-3) is quantum collision-resistant, but only in certain conditions, which make it a little less effective against such attacks.

It is nevertheless believed that a hash function with 256 bits of classical security would still have 128 bits of quantum security:

Algorithm	Key length	Security Level (classical)	Security Level (quantum)
SHA-256	256 bits	256 bits	128 bits

Good hash functions (SHA-2, SHA-3, …) are believed to be resistant to quantum adversaries.

Finally, as we have already seen, Shor’s algorithm allows a quantum circuit to solve discrete logarithm problems in polynomial time, which opens the door to attacks on DH and ECDH with large enough quantum computer, in the same way at they do with RSA or ECC.

Post-quantum cryptography

Quantum computing is still in its infancy. Experiments have been carried out in which operations are executed on a very small number of quantum bits. In 2001, a 7-qubit quantum computer became the first to run Shor’s algorithm and factored … the number 15.

Since then, a lot has progress has been made, especially in the field of topological quantum computing. Google’s Bristlecone 72 qubits processor holds the record as of 2018. Practical and theoretical research are carried on, in effort to develop quantum computers for civilian, business, trade, environmental and security purposes, such as cryptanalysis.

As seen in the previous paragraph, not all security protocols and cryptographic algorithms are born equals: some are believed to be resistant from quantum attacks, while some are already known to be vulnerable.

For example, a recent study has been carried out on quantum attacks on the Bitcoin blockchain (arXiv:1710.10377v1). The study found:

that the hash-based proof-of-work currently used is relatively resistant to substantial quantum speedup;
that the ECC signature scheme used by Bitcoin is much more at risk and could be completely broken by a quantum computer in a early future (less than 10 years by their most optimistic estimate).

Security controls that are known to be highly vulnerable to quantum attack, and can be easily broken by a quantum computer, include:

Cryptosystem that is built on top of mathematical problem such as integer factoring or discrete logarithms. This includes RSA, DSA, DH, ECDH, ECDSA (and other variants of these ciphers). .
Any security protocols that derive security from the above public key ciphers.
Any products or security systems that derive security from the above protocols.

It is important to point out that almost all public key cryptography and protocols today use these types of ciphers.

Some cryptographers are looking at ways to “fight quantum with quantum”, but there are another options. Research is also carried on what is called post-quantum cryptography (although a more precise name might be quantum-resistant cryptography): post-quantum cryptography usually refers to the effort to build classical cryptographic algorithms that are secure against attacks via quantum computing.

Focus is usually made on cryptography based on mathematical problems such as solving systems of multivariable polynomials, finding the shortest distance from a point to an n-dimensional skewed grid of other points, and finding the closest bit string to a set of other bit strings.

One of the front-runners for post-quantum is lattice-based cryptography. Lattice problems are a class of optimization problems on lattices.

As Joshua Holden explains [http://nautil.us] “If Alice wants to send Bob a message, she could identify it with a point in Bob’s n-dimensional grid and then add some “noise” to it by moving it off the grid a small amount. If n is very large and the angles in the grid are skewed—very far from right angles—it seems difficult for Eve the Eavesdropper to figure out Alice’s original point, and a quantum computer doesn’t seem to help much. But if Bob (and only Bob) has a different set of lines drawn through the same points, but with angles closer to 90 degrees, then he has a “trap door” which allows him to recover the point and the message. ”

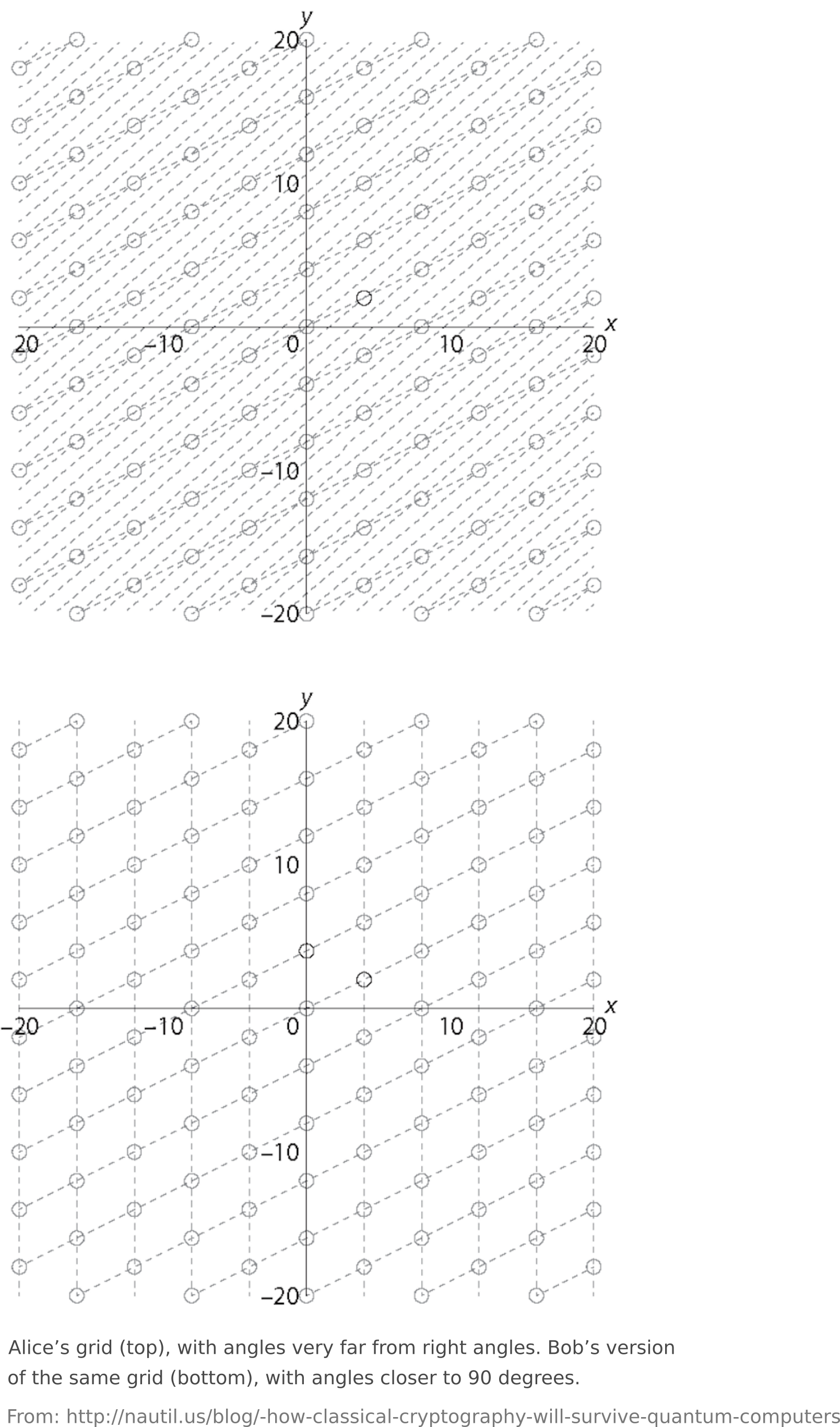
Many lattice-based cryptographic schemes are known to be secure assuming the worst-case hardness of certain lattice problems.

Among them, NTRU is an open source public-key cryptosystem that uses lattice-based cryptography. NTRU (and its variants) have been entered into the Post-Quantum Cryptography Standardization NIST effort to standardize post-quantum cryptography. The Post Quantum Cryptography Study Group of the European Commission is also considering standardization of the provably secure Stehle-Steinfeld version of NTRU.

The security of the NTRU encryption is related to the Closest Vector Problem (CVP) in a Lattice, which is known to be NP-hard.

As a bonus, some NTRU-based cryptosystem are homomorphic (a form of encryption that allows operations on ciphertexts, which, when decrypted, matches the result of the operations as if they had been performed on the plaintext), making them particularly suitable for cloud-computing.

Quantum Key distribution

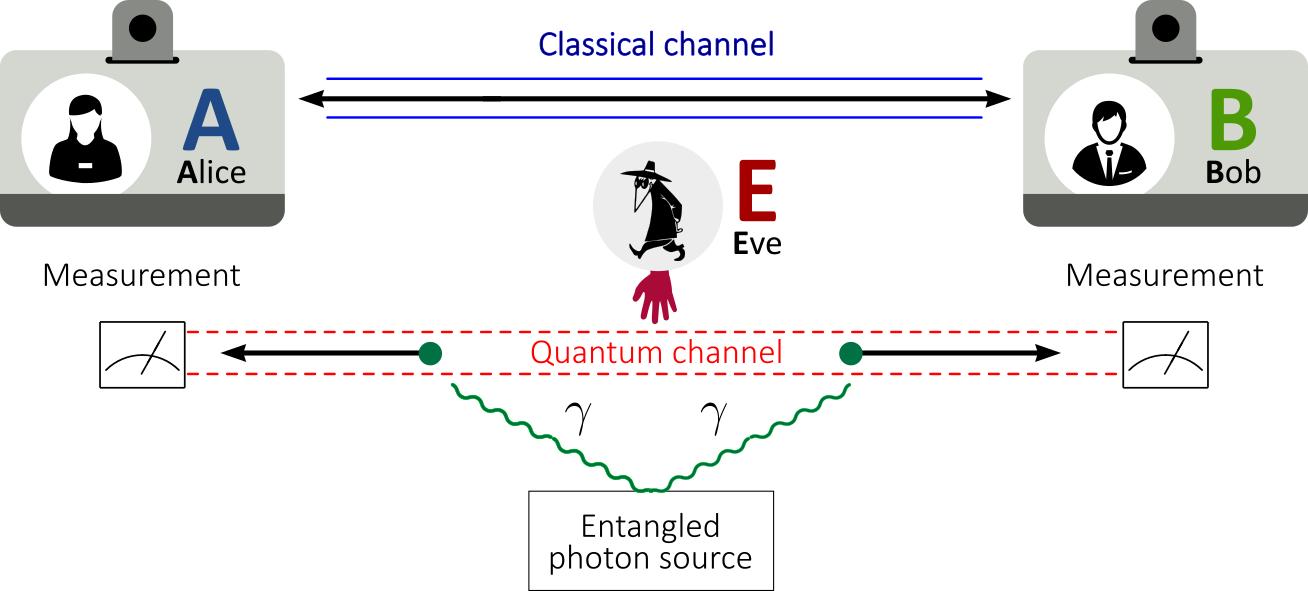
Let’s finish this (long) post with a few information on quantum cryptography. Its purpose is to exploit quantum mechanical properties (entanglement, superposition, measurement and wave function collapse, teleportation, no-cloning theorem, …) to perform cryptographic tasks.

The best known example of quantum cryptography is quantum key distribution which offers, like DH, an information-theoretically secure solution to the key exchange problem.

Indeed, even with the one-time pad (forgetting its practical drawbacks), the secrecy problem is only shifted to the problem of distributing the key in a safe way to the receiver. In principle, a spy can get hold of the share key, copy it and send it on to the receiver.

This is the point where quantum physics enters the stage: if the key distribution makes use of quantum states the spy cannot measure them without disturbing them. Thus principles of quantum mechanics can help to make the key distribution safe. The unique property of quantum key distribution is the ability of the two communicating users to detect the presence of any third party trying to gain knowledge of the key:

A third party trying to eavesdrop on the key must in some way measure it, thus introducing detectable anomalies;
By using quantum superpositions or quantum entanglement and transmitting information in quantum states, a communication system can be implemented that detects eavesdropping.

Just like DH, quantum key distribution is only used to produce and distribute a key, not to transmit any message data. The algorithm most commonly associated with QKD is the one-time pad.

Here is a list of common quantum mechanics properties used to build secure key distribution protocols:

P1 – no-cloning theorem: we introduced this quantum properties in a previous post. It is impossible to create perfect copies of an unknown quantum state. Thus a spy is not able to produce perfect copies of a quantum state in transit in order to measure it, while sending on the original.
P2 – entanglement: as seen in our posts on Bell states and on quantum teleportation, two or more quantum systems can be correlated or entangled. If measurement are being performed on the two entangled subsystems, there will always be a correlation between the outcomes;
P3 – non-orthogonal states cannot be reliably distinguished: Generally speaking, a qubit can be written as $|\psi_i\rangle = \alpha_i |0\rangle + \beta_i |1\rangle$ where $\alpha_i$ and $\beta_i$ are complex coefficients satisfying $|\alpha_i|^2 + |\beta_i |^2= 1$ . It is impossible to distinguish reliably between two states $|\psi_1|\rangle$ and $|\psi_2\rangle$ unless $\langle\psi_1|\psi_2\rangle=1$ (i.e the states are orthogonal);

Causality, though not an ingredient of (non-relativistic) quantum mechanics, is also an important ingredient. Together with the superposition principle, causality can be used for secure key distribution: if the two terms of which a superposition consists are sent with a time delay relative to each other, such that they are not causally connected, the eavesdropper cannot spy on them.

In a typical QKD protocol, Alice and Bob obtain some quantum states and measure them (quantum channel). They then communicate (via a classical communication channel) to determine which of their measurement results could lead to secret key bits:

Note: neither of these two channels need to be secure: the protocol is designed with the assumption that Eve can interfere in any way with both.

The BB84 scheme was the first proposed quantum key distribution protocol (1984, Charles Bennett and Gilles Brassard). This protocol is provably secure, relying on the property P3 seen before: information gain is only possible at the expense of disturbing the signal if the two states one is trying to distinguish are not orthogonal.

For this, one has to encode information in non-orthogonal states. Alice chooses two n-bits long strings $a$ and $b$ ( $a_i$ and $b_i$ being the i-th bit of $a$ and $b$ ).

She encodes this information into the quantum state $\displaystyle |\psi\rangle = \bigotimes_{i=1}^{n} |\psi_{a_i b_i}\rangle$ , where:

$\displaystyle |\psi_{00}\rangle = |0\rangle$ ;
$\displaystyle |\psi_{10}\rangle = |1\rangle$ ;
$\displaystyle |\psi_{01}\rangle = \frac{1}{\sqrt{2}} |0\rangle + \frac{1}{\sqrt{2}} |1\rangle$ ;
$\displaystyle |\psi_{11}\rangle = \frac{1}{\sqrt{2}} |0\rangle - \frac{1}{\sqrt{2}} |1\rangle$ .

The bit $b_i$ (only known by Alice) is what decides which basis $a_i$ is encoded in (either in the computational basis or in the Hadamard basis). The qubits are now in states that are not mutually orthogonal, and thus it is impossible to distinguish all of them with certainty without knowing $b$ .

Practically speaking, photons are shot between parties, and information is encoded along either a rectilinear or diagonal axis.

The BB84 protocol goes like this:

Alice sends $|\psi\rangle$ to Bob over a public quantum channel;
Bob receives a state affected by errors (effect of noise in the channel or of Eve’s eavesdropping);
We know that Eve cannot be in possession of a copy of the qubits sent to Bob, by the no-cloning theorem (property P1), unless she has made measurements. Her measurements, however, risk disturbing a particular qubit with probability 1/2 if she guesses the wrong basis;
As Bob does not know the basis the information was encoded in, all he can do is to select a basis to measure in, either rectilinear or diagonal. Bob chooses $b'_i$ axes and measures the received state along these axes (and gets $a'$ );
Bob announces on the classical public channel that he has received Alice’s transmission;
Bob communicates with Alice (over the same public classical channel) to determine which $b_i$ and $b'_i$ are not equal;
Both Alice and Bob drop the qubits in $a$ and $a'$ where $b$ and $b'$ don’t match;
From the remaining $k$ bits where both Alice and Bob measured in the same basis, Alice randomly chooses $k / 2$ bits and discloses her choices over the public channel;
To check for the presence of an eavesdropper, Alice and Bob compare the subset of bits. If Eve has gained any information about the photons’ polarization, this introduces errors in Bob’s measurements. Other environmental conditions can cause errors in a similar fashion. If more than $p$ bits differ they abort the key and try again. $p$ is chosen so that if the number of bits known to Eve is less than this, privacy amplification can be used to reduce Eve’s knowledge of the key to an arbitrarily small amount at the cost of reducing the length of the key.

There are many other QKD protocols, such as E91, which relies on properties P1 and P2. An Industry Specification Group (ISG) of the European Telecommunications Standards Institute (ETSI) has been set up to address standardization issues in quantum cryptography.

Many experiments have been carried out over the last 10 years, and companies are starting offering commercial quantum key distribution systems (in Switzerland, France, Australia and USA). The 2016 QUESS space mission created an international QKD channel between China and the Institute for Quantum Optics and Quantum Information in Austria. By October 2017, a 2,000-km fiber line was operational between Beijing, Jinan, Hefei and Shanghai. Together they constitute the world’s first space-ground quantum network. It is expected that a European–Asian quantum-encrypted network will by ran by 2020, and a global network by 2030.

Note: A few paragraphs and illustrations of this post are based on wikipedia’s entries on quantum cryptography, ETSI White Paper No. 8 and Nautilus blog (nautil.us/blog).

Leave a Reply Cancel reply