What’s this Higgs boson anyway ?

Recently, there’s been a lot of talk about the Higgs boson. A month ago, both teams from CMS and ATLAS experiments at LHC have announced independently the discovery of a previously unknown boson of mass between 125–127 GeV/c2. The characteristics of this new particle are consistent whith the ones of the Higgs Boson.

Without getting into too much details and technicalities, let’s see what this particle is, what open questions remain. But, before that that, we’ll have pay a little visit to what is called the Standard Model of Particle Physics. If you already know the concepts of fermions, bosons and other gauge fields, feel free to skip these paragraphs.

Fermions

Particle physics distinguishes two classes of particles, according to a quantum property called spin.

The first class, called fermions, is composed of particle with half-integer spin. They were named after the famous Italian-born physicist Enrico Fermi. From the statistical mechanics point of view, they obey Fermi-Dirac statistics.

Elementary particles, such as electrons, muons, neutrinos or quarks, are all characterized by a 1/2 spin. Composite fermions, such as protons, neutrons, or any baryon (triplets of quarks) or nucleus can carry any half-integer spin (1/2, 3/2, 5/2, …).

Particles with half-integer spin are subject to the Pauli exclusion principle: no two identical fermions may occupy the same quantum state simultaneously.

Bosons

The second class of particles, called bosons, is composed of particles with integer spin. They were named after the famous Indian physicist Satyendra Nath Bose.

From the statistical mechanics point a view, they obey another statistics, called the Bose-Einstein statistics. Bosons, may be elementary particles, such as photons or gluons. They also can be composite particles like mesons (quark-antiquarks pairs), such as the $J/\psi$ .

Contrary to fermions, bosons are not subject to the Pauli exclusion principle: two or more bosons can occupy the same quantum state.

The following image sketches the difference between bosons and fermions:

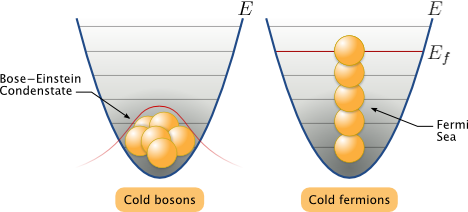
Imagine two apparati, one containing a gas of bosons, while the other one contains a gas of (non interacting) fermions. As the temperature drops near absolute zero, the gas of bosons collapses, forming a Bose-Einstein Condensate. Fermions can’t reach this state, since they can’t occupy the same quantum state. The total energy of the Fermi gas is then larger than the sum of the single-particle ground state. The energy of the highest occupied quantum state is called the Fermi energy.

Very simply speaking, a the most elementary level, one can see fermions as the perfect candidate for building blocks of matter, while bosons are candidates for interactions.

Note: obviously, this would only true for non-composite particles, since mesons are a form of non-baryonic matter and are still bosons.

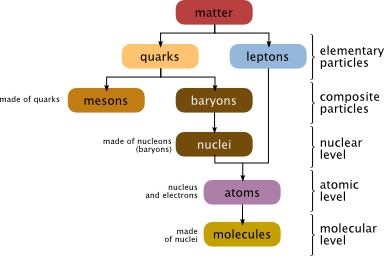
What is matter made of ?

On the scale of elementary particles, matter is composed of elementary fermions, namely quarks and leptons:

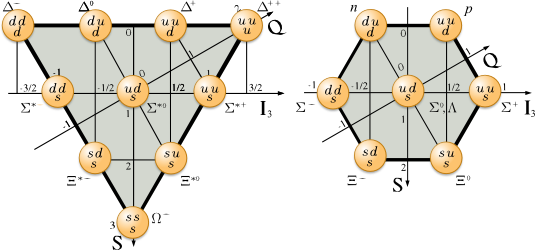
“quark matter” ( $q \bar q$ mesons and $q_1 q_2 q_3$ baryons) is essentially a combination of quarks. The following diagrams illustrate such combinations (here, in the case of u-d-s baryons):

A nucleus is a combinations of nucleons (neutrons and protons), an atom is a combination of a nucleus and electrons (leptons), a molecule is a combinations of atoms, …

How do these particles interact ?

In particle physics, fundamental interactions are the ways that elementary particles interact with one another. An interaction is fundamental when it cannot be described in terms of other interactions.

The four known fundamental interactions, are electromagnetism, strong interaction (“strong nuclear force”), weak interaction (“weak nuclear force”) and gravitation.

With the notable exception of gravitation, all these fundamental interactions have been expressed according to quantum field formulations, namely:

Quantum Electrodynamics (or QED): the quantum field formulation of electromagnetism, which served as a model for all the other theories
Quantum Chromodynamics (or QCD): the quantum field formulation of strong interactions (which used to be my playground in a distant past)
Electroweak model (or GWS): Sheldon Glashow, Steven Weinberg and Abdus Salam have unified both weak and electromagnetism interactions into a single, unified quantum theory, which is now the basis of the standard model of particle physics

Modern physical theories describe reality in terms of fields, e.g., the electromagnetic field, the gravitational field, and fields for other elementary particles. A force carrier (also called gauge boson, we’ll why later on) is a bosonic particle that carries any of the fundamental interactions : elementary particles interact with each other by the exchange of bosons:

Photons: photons are bosons, force carriers of the electromagnetic force
Gluons: the 8 gluons, are bosons that act as the exchange particles for the force between quarks (and actually, between gluons, which makes QCD a fun and tricky theory)
$W^{+}, W^{-}$ and $Z^0$ bosons: these bosons mediate the weak interaction

How can we picture these carriers ? Let’s forget for a minute fields and particles, and imagine a pair of basketball players (seen from above):

At first, let them separately dribble. Each player will follow his path, independently of the another. They are “non interacting players”. Now, imagine them exchanging a ball. Both players will now follow correlated path. They are “interacting players”. Then, give them an heavier ball. Their paths will get closer, because the range of their interaction will became shorter: exchanging an heavy ball over a long distance is harder than with a lighter one.

Well … that’s about the same for particles. Electrically charged particle interact with each other by the exchange of virtual photons, quarks (color-charged particles) interact with each other by the exchange of virtual gluons, etc.

The heavier the gauge boson is, the shorter the range of the interaction, and conversely.

Note: this is not true for QCD, where gluons (which are massless and should have an infinite range of interaction) carry themselves color charges which leads to a property call color confinement.

Instead of images of basketball players, physicists picture these interactions with Feynman diagrams:

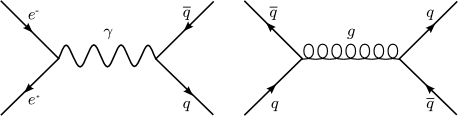
Of course, behind these diagrams hides a few calculations: Feynman diagrams are graphical representations of a perturbative contribution to a probability amplitude of a given quantum system. These can give more headaches to physicists than basketball games, believe me.

Standard Model and and gauge symmetries

As seen in the post on general relativity, there is a strong connection between symmetries and laws of physics. Actually, particle physics laws can be written by solely choosing the simplest mathematical laws that obey observed symmetries (or observed quantities that are conserved). These mathematical expression are called Lagrangians : function that summarizes the dynamics of a system. Given a variational principle and these Lagrangians, physicists are able to formulate all the physical laws, which results, in quantum terms, are probability amplitudes … which are more or less Feynman diagrams.

Let’s start with the mother of all quantum field theories: quantum electrodynamics (QED).

To formulate QED, one has to observe that during electromagnetic interactions the electric charge is a quantity that is always conserved. We know, thanks to the Noether’s theorem, that to a given conserved quantity corresponds a given symmetry (and conversely). In the case of the electric charge conservation, a simple reasoning shows that laws have to be globally invariant under transformations of a semi-simple Lie group named U(1).

But, there is another invariance that laws of electrodynamics must obey: Lorentz invariance. In other words: QED is a relativistic theory. In order to be Lorentz and U(1) invariant, our formulation has to be invariant under all local U(1) transformations (and not only global transformations). A field theory invariant under a continuous group of local transformations is called a gauge theory (hence the name “gauge boson”).

The simplest relativistic Lagrangian invariant under local U(1) transformation can be written as:

$\mathcal{L}_{QED} = i \bar{\psi}\gamma^{\mu}\partial_{\mu}\psi - e \bar{\psi} \gamma_{\mu} (A^{\mu} + B^{\mu})\psi - m \bar{\psi} \psi - \frac{1}{4} F_{\mu\nu} F^{\mu\nu}$

Applying a variational principle (leading to the classical Euler-Lagrange equation) gives

$i\gamma^{\mu}\partial_{\mu}\psi - m \psi = e \gamma_{\mu} (A^{\mu} + B^{\mu})\psi$

The left-hand side is like the original Dirac equation and the right-hand side is the interaction with the electromagnetic field. Bingo 🙂

Note that U(1) has only one generator, which corresponds to the existence of one single type of (massless) photon.

This is so powerful, the same procedure can be followed to build Quantum Chromodynamics: one has simply to build a Lagrangian that is Lorentz invariant and locally SU(3) invariant (color invariance). QCD Lagrangian goes as:

$\mathcal{L}_{QCD} = \bar{\psi}_{i}( i \gamma^{\mu}D_{\mu})_{ij} - m \delta_{ij}) \psi_{j} - \frac{1}{4} G^{a}_{\mu\nu} G_{a}^{\mu\nu}$

Note that SU(3) has 8 generators, which correspond to the existence of the 8 massless gluons.

Its seems that this procedure is just perfect to build field theories with massless gauge bosons (if a mass term is added to the Lagrangian, the symmetry is lost)

And now comes the electroweak model, which unified weak and electromagnetic forces. Mathematically speaking, the unification weak and electromagnetic interactions is accomplished under an SU(2) × U(1) gauge group. There are four corresponding gauge bosons, which is good, but that are also all massless.

Now, that’s a problem, because weak interactions are … weak. And this means that weak gauge bosons have to be quite obese !

So, where does the mass of these gauge bosons come from ?

Houston, we have a problem. To build a local field theory with 3 massive and one massless gauge bosons, we’ll have to introduce something new.

As usual, this will be related to symmetries. But it is can feel a little far fetched. This idea is the following: at temperature high enough, the SU(2) x U(1) symmetry is unbroken, whereas at a critical temperature, the symmetry is spontaneously broken thanks to the introduction of a new field.

This is bold: a completely new field, never observed, to give mass to gauge bosons, that, at the time where the theory was built, were yet to be discovered !

The only things that were sure is that weak interactions existed and that since they were soooo weak, that had to be carried by monstrously heavy particle.

Note: W and Z bosons proved to be 80-90 times heavier than a proton !

Spontaneous symmetry breaking and Nambu-Goldstone bosons

Let’s see how spontaneous symmetry breaking could be a good mass generation mechanism.

First of all, symmetry breaking at lower energies is is not a unusual phenomenon. Water freezing into ice is a good example. Liquid water is quite symmetrical: if you look at the arrangement of individual water molecules, it looks the same in all directions. Now, when water freezes, though, it loses this symmetry. It becomes an ice crystal, with molecules arranged in a regular lattice. This arrangement is actually less symmetrical, because it has symmetries only in certain directions.

Spontaneous symmetry breaking is a mode of realization of symmetry breaking, where the underlying laws are invariant under a symmetry transformation, but the system as a whole changes under such transformations.

One can easily understand the mechanism of spontaneous symmetry breaking watching the buckling of a steel nail. Let’s set the nail vertically. The system is then symmetrical with respect to rotations around the axis of the nail. Now, let’s apply a vertical compressive force on the nail.

As long as the compressive force is less than a critical value $F_{crit}$ , the potential energy minimum is symmetrical with respect to the rotations around the axis. Now, if this force exceeds a critical value, the nail buckles and the minimum potential energy is no longer symmetrical with respect to the rotation, while the form of potential energy is (and the set of its minima exhibit the original rotational symmetry) :

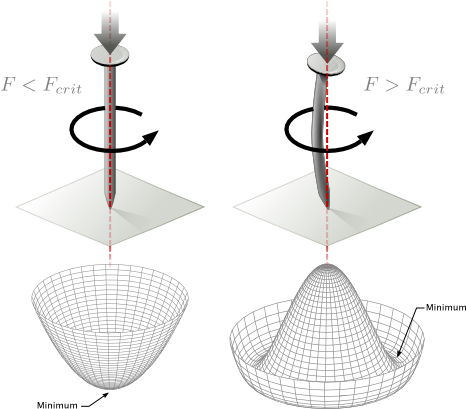
The Goldstone theorem applies to generic continuous symmetries which are spontaneously broken. It states that new massless bosons appear: there is one particle (called a Nambu–Goldston boson) for each generator of the broken symmetry.

Then, in 1964, three teams proposed related but different approaches to explain how mass could arise in local gauge theories. These three, now famous, papers were written by Robert Brout and François Englert, Peter Higgs, and Gerald Guralnik, C. Richard Hagen, and Tom Kibble, and are credited with the prediction of thea mechanism which provides the means by which gauge bosons can acquire non-zero masses in the process of spontaneous symmetry breaking. They showed that Goldstone bosons need not occur when a local symmetry is spontaneously broken in a relativistic theory. Instead, the Goldstone mode provides a massive field.

Now, we’ve got something 🙂

Electroweak theory and Higgs mechanism

Steven Weinberg and Abdus Salam proposed that the mass of the three weak force carriers could be the result of a similar process. To explain this, they invoked the additional field proposed by Peter Higgs, called the Higgs field. Technically, in the standard model, the Higgs field is an SU(2)_L doublet, a complex spinor with four real components:

$\varphi = \frac{1}{\sqrt{2}} \left( \begin{array}{c} \varphi^{+} \\ \varphi^{0} \end{array} \right)$

The trick is thus to add a spontaneous symmetry breaking to the electroweak SU(2) x U(1) gauge theory in order to give mass to carriers of the weak interaction while preserving the massless characteristic of the electromagnetic interaction carrier.

Applying the Goldstone theorem to a spontaneously broken, globally invariant SU(2) x U(1) model should give birth to four massless bosons. In the case of a spontaneously broken SU(2) x U(1) gauge symmetry, the goldstone bosons are “eaten” by gauge bosons: after symmetry breaking, these three of the four components of the Higgs field mix with the $W^{+}, W^{-}$ and $Z^0$ bosons, and are only observable as spin components of these weak bosons, which are now massive; while the one remaining degree of freedom becomes .. the Higgs boson.

It leaves us with massive $W^{+}, W^{-}$ and $Z^0$ bosons, and a Higgs boson. The electromagnetic interaction carrier ( $\gamma$ boson) remains massless.

And … voilà !

We can think of the Higgs field as causing a hill of potential energy. At each point in the field, a particle has a certain mass. At the top of the field, at high energies, the mass is zero. Around the bottom of the hill are different, non-zero masses:

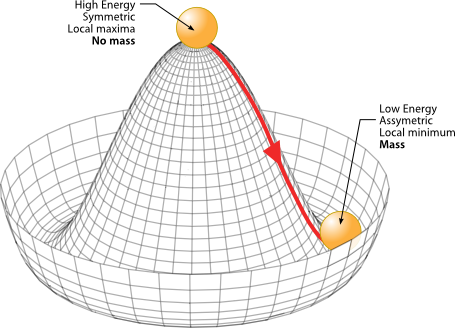
With the Higgs field, all four weak force particles started out with zero mass, at the high energies of the Big Bang, but this symmetry was broken when energy intensity fell, and three of the particles gained mass.

What about fermions ?

In spite of the introduction of spontaneous symmetry-breaking the mass terms of the Lagrangian yet oppose another experimentally observed invariance, called chiral (gauge) invariance.

An easy solution to give mass to fermions it to introduce some kind of Yukawa coupling between the fermion field $\psi$ and the Higgs field $\phi$ .

In particle physics, Yukawa’s interaction (named after the Japanese physicist Hideki Yukawa), is an interaction between a scalar field $\phi$ and a Dirac field $\psi$ of the following form:

$\mathcal{L}_{Yukawa} = G_{\psi} \bar{\psi}\phi\psi$

Initially, the Yukawa interaction was be used to phenomenologically describe the strong nuclear force between nucleons, mediated by pions. Nowadays, the Yukawa interaction also used in the Standard Model to describe the coupling between the Higgs field and massless quark and lepton fields. Through spontaneous symmetry breaking, these fermions acquire a mass proportional to the vacuum expectation value of the Higgs field. Adding this Yukawa coupling between fermions and the Higgs field gives a nice mechanism to give mass to fermions, while preserving chiral invariance.

And then ?

The Higgs mechanism that we briefly described is the simplest trick that one can find to give mass to fermions (while preserving chiral invariance) and to electro-weak bosons (while preserving a massless electromagnetic boson). This allows one to write down physics in terms of relativistic gauge-invariant quantum field theory (aka Standard Model) … which is the best fundamental theory we have so far to describe the universe at small scales.

Note: there are actually more complex Higgs models where several Higgs bosons would exist. But physicist are generally inclined to simple ideas (Occam principle).

Even if it feels a little ad-hoc, the idea of a spontaneous symmetry breaking is a very fruitful one. It introduces the notion of phase(s) transition(s): from a “low temperature, unsymmetrical world”, one can think of a “high temperature, highly symmetrical universe” where all forces are unified:

This is the basis of the Grand Unified Theory (GUT) ideas.

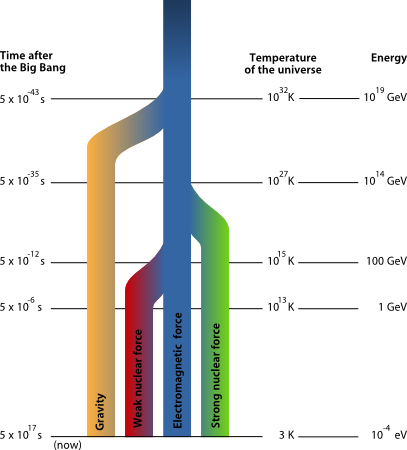
But, as fruitful as they may be, these ideas are not enough to give a full description of what can be observed at the low-scale (high energy) level. For example, even if the Higgs mechanism is the correct mechanism to give mass to particles, in itself, it gives absolutely no clue as to:

What mass is: we still don’t actually know what a mass is (and I’m not even getting into the difference between inertial and gravitational mass…)
Where do the values of masses come from. Even with a Higgs mechanism, we still don’t know why particles carry the masses we measure. Even the Higgs mechanism can’t tell what the mass of the Higgs boson is. That’s one of the many reasons why it is so hard to find.

In simple terms, even it the Higgs boson was seen at LHC, what would make me immensely happy, is signs of new physics: new materials to get fresh ideas to go beyond the standard model 🙂

3 thoughts on “What’s this Higgs boson anyway ?”

Riz Haider 17 February 2013 Reply

Driven by intense curiosity and a non-scientific background I finally found an explanation of the standard model and beyond which finally shed a tiny beam of undertstanding. Many thanks, Fred.
Pingback: What’s this Higgs Boson anyway? | Concrete Dreams
David Love 14 June 2016 Reply

Would you please tell me what the potential is at the top of the so called mexican hat? I realize the trough value of v is 246 GeV.

Thanks,
David Love

3 thoughts on “What’s this Higgs boson anyway ?”

Leave a Reply Cancel reply