Basic principles of General Relativity

As promised a couple of posts ago, here are a few words on General Relativity. I’ll try to concentrate on the principles by not focusing (too much) on technicalities.

Keeping this post concise is quite a challenge, because of the incredible beauty lying in the physics and mathematics of General Relativity. A thing of beauty is a joy forever…

Symmetry and relativity

Symmetries and laws of physics are deeply connected. There exists an extremely important result called Noether’s theorem, which states that such symmetries also imply the conservation of physical quantities.

For example, energy is conserved if the laws describing a system at a given time are still the same at another time: time-translation invariance of the laws of physics implies the conservation of energy. The same link exists between conservation of linear momentum and space-translation invariance, or between conservation of angular momentum and rotations.

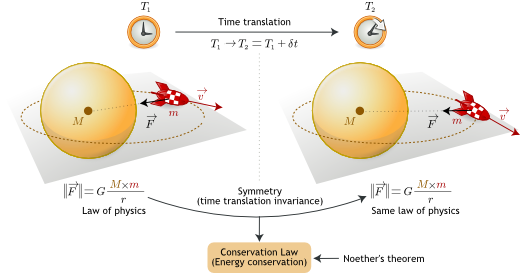
Symmetry principles are not just statements about how scientists should write laws. They make testable predictions about how nature behaves. Conversely, they constitute a formidable tool to formulate physical theories from experimental data: what truly and only characterize a physical system is what doesn’t change when one changes his point of view of that system. Give to a theoretical physicist a quantity that is conserved, he’ll find a symmetry.

That’s extremely powerful, because symmetries and variational principles are all that is needed for a theoretician to build accurate descriptions of how Mother Nature works.

Relativity is a particular form of symmetry: a principle of relativity is the requirement that the laws of physics, have the same form independently of frames of reference.

Historically, many forms of these principles were introduced since: Galileo‘s relativity, Einstein‘s Special and General relativity, …

Galilean relativity

Let’s go back to 1632 and Galileo’s “Dialogue Concerning the Two Chief World Systems“. In his seminal work, Galileo introduced a relativity principle which, in today’s formulation, could be expressed as follows:

There exists an absolute space. A Galilean inertial frame is a reference frame in relative uniform motion to absolute space
All inertial frames share a universal absolute time

In the absence of external interactions, free bodies are following straight lines at constant velocity (or are at rest). Any influence that causes a free body to deviate from this state is called a force. Galilean relativity states that the laws of physics take the same form all inertial frame. In simple mathematical terms, the laws of physics are invariant under transformations of this form (Galilean transformations):

$\left\{ \begin{array}{llll} x' &=& x -vt \\ y' &=& y \\ z' &=& z \\ t' &=& t \end{array} \right.$

Newton’s law of universal gravitation

Let’s jump to 1687. Newton‘s masterpiece, “Philosophiæ Naturalis Principia Mathematica“, has set the grounds of what is now called classical mechanics.

Based on Galileo’s reflections, Newtons defined three laws:

Fist law (inertia): it is a restatement of Galileo’s relativity. An object at rest tends to stay at rest, or if it is in motion tends to stay in motion with the same speed and in the same direction unless acted upon by a sum of physical forces
Second law (motion): a body will accelerate with acceleration proportional to the force and inversely proportional to the mass:

$F_i = m \frac{d^2x_i}{dt^2}$
Third law (reciprocal actions): every action has a reaction equal in magnitude and opposite in direction.

Newton’s law of universal gravitation completes these principles. Every point mass attracts every single other point mass by a force pointing along the line intersecting both points. The force is directly proportional to the product of the two masses and inversely proportional to the square of the distance between the point masses:

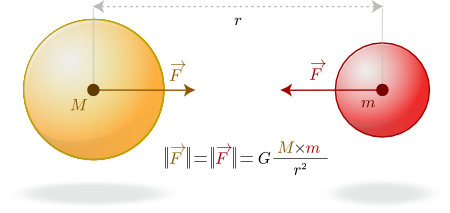
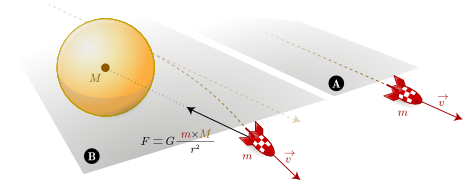
The following picture illustrates Newton’s theory:

Case A: in absence of external influence, a free body follows a straight line at constant speed
Case B: under the influence of gravity, the body follows a trajectory explained by the combination of Newton’s second law of motion and Newton’s law of universal gravitation.

Based on this work, Newton was able to prove that Kepler’s laws of planetary motion, which match Tycho Brahe‘s observations, were consequences of his own laws of motion and universal gravitation.

What is wrong with this ?

Newton’s theory is accurate enough for many practical purposes, and is still widely use. Nevertheless, in light of today’s knowledge, major concerns (experimental and theoretical) with this theory lead scientists to find a totally new paradigm.

From an experimental point of view: Newton’s theory cannot cope with today’s high precision observations. For example, it doesn’t fully explain the precession of the perihelion of the planet Mercury, or the deflection of light rays by gravity
From a theoretical point of view: Newton’s concept of action at a distance is quite unsatisfactory. Furthermore, it require that the gravitational force be transmitted instantaneously, which is known now to be impossible.

To go any further, one has to revise both Galilean relativity (absolute time and space) and Newtonian gravitation (action at a distance ruled by an inverse square law)

Einstein’s Special Relativity

By the end of the 19th century, several interferometer-based experiments (Michelson & Morley, Fizeau, …) were carried out.

The results of these experiments were quite surprising, and, at the time, there were no possible explanation within the corpus of available theories. These experiments are now referred to as “the kicking-off point for the theoretical aspects of the Second Scientific Revolution”.

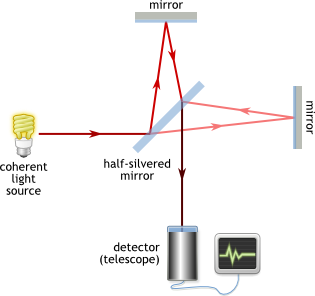
There is no such thing as the luminiferous aether
The speed of light is the same for all inertial observers regardless of the state of motion of the source.

This very last observation is of particular importance, since it is incompatible with the Galilean-transformation invariance requirement. Great minds, such as Poincaré, Lorentz or Einstein tackled this problem.

Einstein postulated in 1905 the following:

The speed of light is a fundamental constant (invariant)
The physical laws (including the constancy of the speed of light) are independent from the choice of inertial system

To build a new framework for physics, compatible with these propositions, Einstein realized than one has to drop Galilean relativity, and proposed a new form a relativity (now called Special Relativity). Within this theory, all physical laws must be invariant under a new group of symmetry, called Lorentz transformations:

$\left\{ \begin{array}{llll} x' &=& \gamma (x -vt) \\ y' &=& y \\ z' &=& z \\ t' &=& \gamma (t - v x / c^2) \end{array} \right.$

where $\gamma = \frac{1}{\sqrt{1-(v/c)^2}}$ and $v$ is the relative velocity between two observers.

These transformations are quite different from Galilean’s. Time and space coordinates are intertwined, resulting in a radically new concept: spacetime. Time and space are not absolute concepts anymore. Speed of light is. I’ll try to write a post sometimes on all the consequences of this (relativity of simultaneity, length contraction, time dilatation, …)

Spacetime is a mathematical model that combines space and time into a single continuum. It is a 4-dimensional space (named Minkowski space), where each point (called “event”) is a set of 4 coordinates:

$(x^\mu) = (x^0,x^1,x^2,x^3)$ where $x_0 \equiv ct,\; x_1 \equiv x,\; x_2 \equiv y,\; x_3 \equiv z$

At this point, for the sake of simplicity and homogeneity, we will introduce “God’s units” where $c \equiv 1$ .

In these units, any interval between two events is given by:

$ds^2 = \eta_{\mu\nu} dx^\mu dx^\nu = dt^2 - (dx^2 + dy^2 + dz^2)$

where:

$\eta_{\mu\nu} = \left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1\\ \end{array} \right]$

Within this formalism, a light cone is the surface describing the temporal evolution of a flash of light in Minkowski spacetime. This can be visualized in 3-space if the two horizontal axes are chosen to be spatial dimensions, while the vertical axis is time:

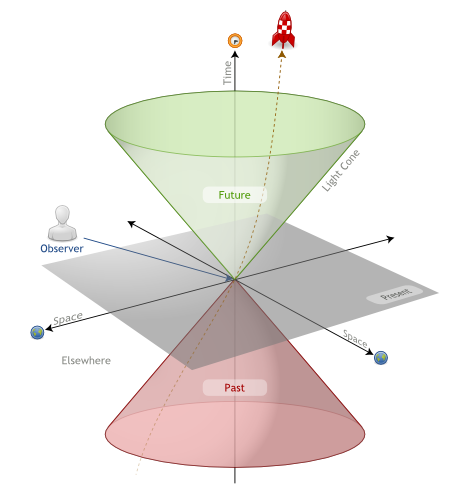
This construction brings to spacetime a very particular structure called causal structure. This is a major “contributor” to the arrow of time. Relatively to a given event E, the light cone classifies events into distinct categories:

Events on the future light cone
Events on the past line cone
Events inside the future light cone are those affected by material particle emitter at E
Events inside the past light cone are those that can emit a material particle and affect the present
All other events, in the absolute elsewhere, cannot affect or be affected by E

A spacetime interval $ds^2$ is said to be:

Time-like if $ds^2 > 0$
Light-like (or null) if $ds^2 = 0$
Space-like if $ds^2 < 0$

Similarly, a smooth regular curve will be classified depending on their tangent vectors. Such a curve is:

Chronological or time-like if the tangent vector is timelike at all point in the curve
Spacelike if the tangent vector is spacelike at all points in the curve
Causal (or non-spacelike) if the tangent vector is timelike or null at all points in the curve

More specifically, a curve is

Future-directed if, for every point in the curve, the tangent vector is future-directed
Past-directed if, for every point in the curve, the tangent vector is past-directed

Einstein’s General Relativity

It is now time to introduce gravity. Einstein quickly realized than Newtonian gravitation is not compatible with his Special Relativity. On one hand, Newton’s actions at a distance are instantaneous, on the other, a simple consequence of Lorentzian invariance is that no information can travel faster than light.

In 1915, Einstein introduced its General Relativity theory. In this theory, the effects of gravitation are ascribed to spacetime curvature instead of a force. How he came to this conclusion starting from the equivalence principle (identification of free fall with inertial motion) is in itself a fabulous story.

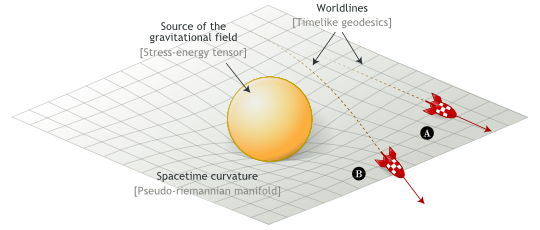
Einstein proposed that spacetime is curved by matter, and that free-falling objects are moving along locally straight paths in curved spacetime. These straight paths are called geodesics. In abscence of gravity, physics is described by Einstein’s Special Relativity. In Minkowski spacetimes, geodesics are plain straight lines.

A Minkowskian spacetime is actually a flat pseudo-euclidean space. Technically speaking, this is the simplest form of pseudo-riemannian manifold.

Einstein postulated that spacetime is a (pseudo-riemannian) manifold. Simply speaking, these are curved spaces which can always be locally approximated by flat pseudo-euclidean spaces (Minkowski spacetimes).

To deal with these geometry, one has to introduce new mathematical objects: tensors. Simply speaking, tensors are geometric entities that extend the notion of scalars, vectors and matrices. These are the natural objects to describe quantities in a relativistic way: tensors themselves are independent of a particular choice of coordinate system.

To express his field equations, Einstein introduced a particular tensor, denoted $T^{\mu\nu}$ and called stress-energy tensor. It is a quantity that describes the density and flux of energy and momentum in spacetime.

Then, he connected stress-energy tensors to local properties of spacetime (curvatures):

$G_{\mu\nu} + \Lambda g_{\mu\nu} = \frac{8\pi G}{c^4} T_{\mu\nu}$ where $G_{\mu\nu} = R_{\mu\nu} - \frac{1}{2} Rg_{\mu\nu}$

Theses field equations mean than energy / mass and momentum proportionally curves spacetime. In absence of gravity (A), spacetime is a flat Minkowskian manifold and free bodies follows straight line. In presence of gravity (B), spacetime is curved and free bodies follow geodesics.

This is a big paradigm shift. Instead of thinking of gravity as a force pulling objects (instantaneous action at a distance), hence causing them to travel along curved paths in a 3-dimensional flat space, one has to think of objects traveling along the straightest paths (geodesics) in a 4-dimensional spacetime curved by the presence of energy and momentum. For example, the path of a planet orbiting around a star is the projection of a geodesic of the curved 4-dimensional spacetime geometry around the star onto 3-dimensional space.

I tried to visually sum up these results in the following picture:

I guess this will be all for tonight as it is now quite late (3:30am). I’ll need a shot of caffeine tomorrow morning. But it is already enough to kick Tony Stark’s ass (see previous posts). More on a the consequences (and limitations) of this formalism in another post …

Credits: jEsuSdA 8 ) for the rocket icon.

1 thought on “Basic principles of General Relativity”

jEsuSdA 8) 17 May 2010 Reply

Wow!!!

What a great surprise to found my rocket icon in these nice illustration!

Great work!
Nice result!

Thank you for reuse my work. 😉

1 thought on “Basic principles of General Relativity”

Leave a Reply Cancel reply