Information and quantum mechanics (part 1)

Okay, at last, a first post about information and quantum mechanics. Let’s begin with the very basic building blocks of all this: quantum states.

A qubit is a short for “quantum bit”. It is to quantum information what a bit is to computer information. Bits and qubits are nevertheless quite different. A computer bit is either a 0 or a 1 (switch off/on, true/false, etc.) whereas a qubit is a superposition of these two orthogonal states. It is a single piece of information with a probability of being true.

In more formal terms, quantum information is described by state vectors in a 2-level quantum mechanical system. In this post, we’ll go into what a “quantum state” is.

The classical world

The simplest classical system is composed of a single non-relativistic particle. Its motion is easily described by the evolution of its coordinates and momentum as a function of time.

This can be generalized to complex systems with the introduction of generalized coordinates and momenta .

The space of all the possible positions that the physical system may attain is called the configuration space. For a single non-relativistic particle, this space is simply . For a n-particles system, this would be .

To take account of both generalized positions and momenta, one has to extend that to introduce a larger manifold called the phase space. Each point of the phase space correspond to a given set of coordinates and momenta .

The dynamics of the physical system is given by all the possible trajectories inside the phase space. It is ruled by the existence of a relation connecting coordinates and momenta formally called an Hamiltonian: .

The equation of motion is given by a variational principle called the principle of least action. Simply speaking, it states that Mother Nature is a big fat lazy girl: among all the possible paths inside the phase space, she will choose the one that minimizes her efforts.

The equation allows one to calculate the dynamical state of the system at time given that its the initial state is known at time .

Practically speaking, the initial state is usually not perfectly known. It is measured by the mean of an experimental apparatus and is actually known within a margin of error given by the precision of this apparatus. From a theoretical point of view, it means that the inital state is known to be somewhere within a defined small hypervolume inside the phase space.

If, at time the system is in two radically different position inside the phase space given two initial states inside that same small hypervolume, the system is said to be chaotic. Even so, the system is still deterministic: if the initial states is perfectly determined, the state at will be perfectly determined.

To sum up, the dynamical state of a classical physical system is fully characterized by its initial state . The values of the measurable quantities (observables) and are thus functions of . One can say that and are the values of the observables and at time for the prepared state .

Now, imagine an experiment where we conduct a series of measures of and at a given fixed time and where the initial state is random. This initial state is called a mixed state, as opposed to pure (defined) states like : it is a statistical mixture of pure states. Both and are now random variables. Even though a single measurement cannot be predicted, on can measure the expectation values of the observables in the state : and .

Observables and states

Now, let’s jump into the quantum world. Here, even pure states show statistical behaviours: regardless of how carefully we prepare the initial state of the system, measurement results are generally not repeatable. This is not the weird prediction of some kind of crackpot theory from a mad scientist. This is just… Nature at work.

At the quantum level, one must understand the results of the measurements of an observable A as a statistical mean. And this mean is what physical theories have to predict. Many experiments have been conducted, setting the fundations of quantum mechanics. I strongly recommend reading about Stern-Gerlach and Bell test experiments.

What are these observations telling us ? Well, many many fundamental things. Among others:

For any observable A, it is possible to prepare a pure state such that A has a fixed value in this state: if we repeat the experiment several times, each time measuring A, we will always obtain the same measurement result, without any random behaviour. Such pure states are called eigenstates of A and the associated values of A are called eigenvalues.
One cannot prepare a state such that both the position measurement 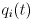and the momentum measurement 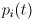give both well defined results at the same time: at least one of them will exhibit a random behaviour. This what the famous Heisenberg uncertainty relations are about. In terms of state, it means that it is generally impossible to prepare a simultaneous eigenstate for all observables.
The results of these experiments exhibit linear properties. Mixed states are linear combination of pure states
It is unavoidable that performing a measurement on the system changes its state: after measuring an observable A, the system will be in an eigenstate of A.

All these results lead to the description of quantum states in terms of vector and observables in terms of linear operators.

Bra-Ket notation

In more technical terms, calculations in quantum mechanics make use of Hilbert spaces, vector, linear operators, inner products, dual spaces, and Hermitian conjugation.

Quite some times ago, Paul Dirac invented a notation to describe quantum states, known as bra-ket notation. Yes, this is some kind of nerdy british sens of humor 😉

The variable name used to denote a vector (which corresponds to a pure quantum state) is denoted by $|\psi\rangle$ (where the “ $\psi$ ” can be replaced by any other symbols, letters, numbers, or even words). Instead of vector, the term ket is used synonymously.
Kets are elements of Hilbert spaces (usualy denoted by $\mathcal{H}$ )
bra are elements of the dual space of $\mathcal{H}$ . They are denoted by $\langle\phi|$ .
Inner products (also called brackets) are written : $\langle \psi|\phi\rangle$ .

Quantum states

As soon as a basis is chosen for the Hilbert space of the system to be described, then any ket can be expanded as a linear combination of those basis elements. The choice of a basis is called a representation. Symbolically, given the chosen basis $|{k_i}\rangle$ , any ket $|\psi\rangle$ can be written as:

$|\psi \rangle = \sum_i c_i |k_i\rangle$

where $c_i$ are complex numbers. In physical terms, $|\psi\rangle$ has been expressed as a quantum superposition of the states $|{k_i}\rangle$ .

We’ll see that expansions of this sort play an important role in measurement in quantum mechanics. In particular, if the $|{k_i}\rangle$ are eigenstates (with corresponding eigenvalues $k_i$ ) of an observable A, and that observable A is measured on the normalized state $|\psi\rangle$ , then the probability that the result of the measurement is $k_i$ is $|c_i|^2$ (assuming the normalization condition $\langle k_i|k_j\rangle = \delta_{ij}$ ).

$\mathcal{P}(k_i, \psi) = | \langle k_i | \psi \rangle |^2 = \left| \sum_j c_j \langle k_i|k_j\rangle \right|^2 = |c_i|^2$

But we’ll get into how to choose a basis (and observables), mixed states, measurement and probabilities in a next post…

Leave a Reply Cancel reply