On hidden realities (part 2)

This is the second part of a series of posts on (a few selected) hidden realities : many-worlds interpretation of quantum mechanics, multiverse linked to the space-time geometries and dynamics, higher dimensional multiverse, holographic multiverse and simulated multiverse.

For the previous posts, please see:

On hidden realities (part 1) – Many-worlds interpretation of quantum mechanics

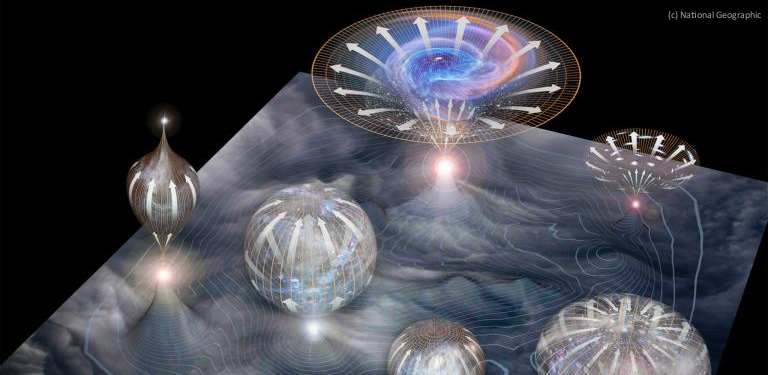
Space-time geometry

General relativity (see this old post for a very brief introduction) is a geometric theory of gravitation. From what we know, and even if many unanswered questions remain (the most fundamental being how to reconcile general relativity with quantum physics), it is the simplest theory consistent with experimental data.

At the heart of general relativity lies the notion of space-time. It is a mathematical model that combines space and time into an interwoven continuum. Technically speaking, Einstein’s theory describes space-time as a a (pseudo-riemannian) manifold.

Einstein’s field equation links the density and flux of matter-energy ( $T^{\mu\nu}$ stress-energy tensor) and the curvature of space-time:

$G_{\mu\nu} + \Lambda g_{\mu\nu} = \frac{8\pi G}{c^4} T_{\mu\nu}$

where $G_{\mu\nu}$ is Einstein’s curvature tensor and $\Lambda$ is the cosmological constant (which was at first omitted by Einstein in what he later called the “greatest mistake of his life”).

In absence of matter-energy, space-time is described by a flat pseudo-euclidean manyfold. More precisely, it is describe by Minkowski’s space-time from special relativity).

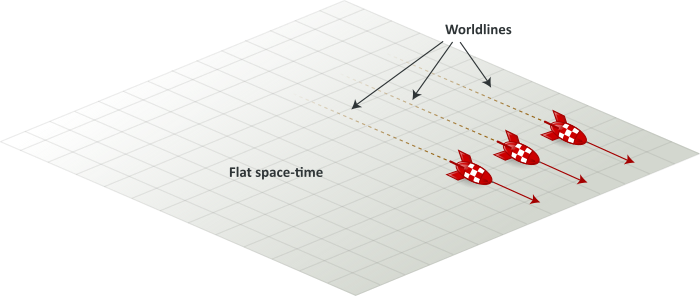
In such space-time, the trajectory of a free (i.e. non-accelerating) particle is a straight line : the shortest path between two points.

In presence of a source of gravity, space-time is described by a curved pseudo-riemanian manifold, which solves Einstein’s field equation:

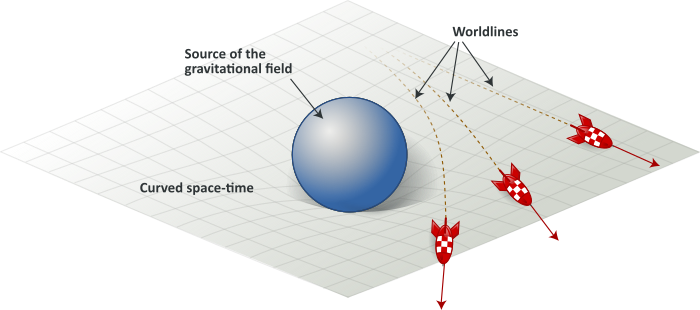
In curved spaces, geodesics are the generalization of the notion of straight line in flat spaces. Timelike geodesics in general relativity describe the motion of a inertial particles. In the above illustration, the rockets’ paths are “straight lines” in a curved space-time.

Geometry of Einstein’s field equation

There are many solutions to Einstein’s field equation, corresponding to different sets of conditions (assumptions on the distribution of matter-energy for example). Each solution describes a particular geometry of space-time. Their dynamics is the cornerstone of relativistic cosmology.

Einstein’s field equation can be written in terms of tensors, or developed as a system of 10 nonlinear partial differential equations in 4 independent variables. Such a system is very difficult solve. Finding exact solution usually requires specific physical conditions, sometimes with simplifying assumptions.

There are two ways to search for these solutions:

fixing the form of the stress–energy tensor and studying the solutions (i.e. space-time geometries)
fixing some geometrical properties of a given space-time and finding a matter source that could provide these properties

In the first case, one usually assumes physical conditions, either observed or simplified ones.

In the second case, there is a wide liberty. For example, one can assume that the universe is homogeneous, isotropic, and accelerating and try to realize what matter can support such a structure (dark energy).

Let’s point out a few Einstein’s field equation exact solutions:

Minkowski solution – which describes an empty space-time with no cosmological constant
Schwarzschild solution – which describes the geometry of space-time around a spherical mass
Kerr solution – which describes the geometry of space-time around a rotating object
Reissner–Nordström solution – which describes the geometry around a charged spherical mass
Kerr–Newman solution – which describes the geometry around a charged, rotating object
Friedmann–Lemaître–Robertson–Walker solution (or FLRW) – which describes the universe an homogeneous, isotropic expanding or contracting fluid. In cosmology, these fluid solutions are often used as cosmological models. Indeed, this model is sometimes called the Standard Model of cosmology
De Sitter solution – which describes as spatially flat universe and neglects ordinary matter. In this solution, the universe is dominated by the cosmological constant. It is thought to correspond to dark energy in our universe or the inflaton field in the early universe (seen the “Inflation” paragraph later on)
Anti-De Sitter solution – which describes a universe with a negative (attractive) cosmological constant, corresponding to a negative energy density and positive pressure of the vacuum. Anti-De Sitter (AdS) is best known in for its role in string and quantum gravity theories, namely through the AdS/CFT correspondence and the holographic principle (we’ll get on this subject in a later post of this series on “hidden realities”)

In fact imagination (also called mathematics) is only limited by physics: one has to ask oneself whether such solution (universe) corresponds to actually possible physical conditions or not.

Solutions can indeed exhibit causally “suspect” features such as closed timelike curves or universes with points of separation (“trouser-worlds”, which are usually ruled out).

Gödel universe is one of them. It describes a universe with a privileged direction (roughly speaking, a universe with a rotating axis). Among many strange properties, Gödel’s universe exhibits (a lot of) closed timelike curves, which would allow some forms of time travel :

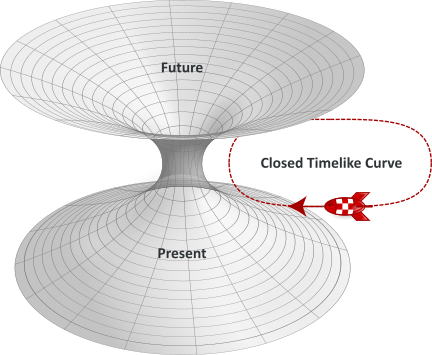
In this universe, there is actually no physical way to define whether a given event happened “earlier” or “later” than another event. Einstein himself (who knew Gödel very well) wrote: “Such cosmological solutions [ … ] have been found by Mr. Gödel. It will be interesting to weigh whether these are not to be excluded on physical grounds.”

Thus, some physicists add “good-sense” conditions. For example, we should mention Igor Novikov‘s consistency principle. This principle aims to solve time-travel paradoxes. It assumes either that there is only one timeline, or that any alternative timelines (such as those postulated by the many-worlds interpretation of quantum mechanics) are not accessible (event with null probability).

One could also assume that solutions should be a Lorentzian manifolds, i.e. smooth manifolds. But it turns out that solutions which are not everywhere smooth can also be very fruitful. Which leads to our next paragraph on singularities.

Singularities

A singularity is a location where the curvature of space-time becomes infinite (for all coordinate systems). In this place, space-time even stops being a manifold. But infinity is one of the things physicists dislike most: they usually don’t exist in the observable world. Most of the time, this is a sign for a missing piece in the theory. Indeed, singularities occur in extreme conditions, where quantum effects dominate. This is somehow general relativity crying for help and stopping being relevant. It’s a call for quantum gravity, a theory we barely have clues about.

This doesn’t stop physicist to tackle this problem. Either in making semi-classical calculations, building (hopefully consistent) theories from the ground up … or observing Mother Nature under extreme conditions and looking for new physics.

Let’s get back first to general relativity and see how it behaves. Singularities can be found in the Schwarzschild metric, the Reissner–Nordström metric, the Kerr metric, the Kerr–Newman metric, …

The first step towards a mathematical characterization under which circumstances general relativity breaks down was achieved in the Penrose-Hawking singularity theorems. In this set of theorems, Roger Penrose and Steven Hawking proved that, under very general conditions, singularities in any general relativity-like theories are ineluctable.

Penrose theorem mostly deals with black holes, whereas Hawking’s deals with the universe as a whole (Big Bang) and works backwards in time (Big Crunch). Of course, keep in mind that these theorems arose from general relativity alone and these results probably break down when quantum physics is somehow added. Hawking actually revised his own position later on, stating “that there in fact no singularity at the beginning of the universe“.

Singular objects and singular events

As we have seen, general relativity cannot be used solely to show a singularity. Because of this, I think we’d rather speak of “singular objects” and “singular events” – uncanny stellar objects and events – than “singularities”. These singular objects would be:

And singular events would be:

We will deal with singular events later on, at the “Relativistic cosmology” paragraph.

Let’s start with huge beasts: black holes. A black hole is usually defined as regions of space-time exhibiting extreme gravitational effects, caused by the collapse of a huge stellar object:

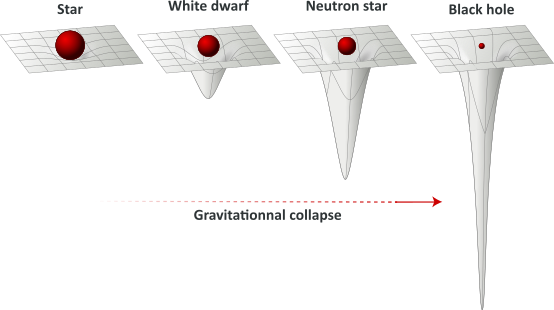
Stars are formed from the collapse of interstellar matter. The compression caused by this collapse raises the temperature until nuclear reactions ignite. The collapse comes then to a halt : the outward thermal pressure balances the gravitational forces and the star reaches a dynamic equilibrium. When all its energy sources reach exhaustion, the equilibrium is broken. The star – depending of its initial mass – will either expand or collapse (again), reaching new states of its evolution. These “stellar remnants” could then be:

Black holes

The Schwarzschild radius is the radius of a sphere such that, if all the mass of an object were to be compressed within it, the escape velocity from the surface of the sphere would equal the speed of light. Once a stellar remnant collapses below this radius, light cannot escape and the object is no longer directly visible, thereby forming a black hole. This radius defines a perimeter called the “event horizon” (more on this later):

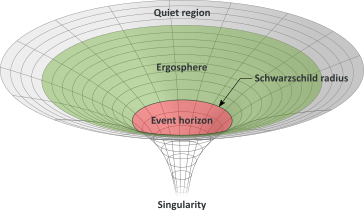
The no-hair theorem states that a black hole has only three independent physical properties: mass, charge, and angular momentum. These properties are very special since they are visible from outside a black hole. A charged black hole would then repels or attracts other charges just like any other charged object.

The simplest static black holes (also called Schwarzschild black holes) have mass but neither electric charge nor angular momentum. According to the no-hair theorem, this means that there is no observable difference between the gravitational field of such a black hole and that of any other spherical object of the same mass. The popular notion of a black hole “sucking in everything” in its surroundings is therefore only correct near the Schwarzchild radius. Far away, the external gravitational field is identical to that of any other body of the same mass (called quiet region). In between lies the ergosphere, where it would theoretically be possible to harness energy and mass from a (rotating) black hole.

Just like space-time around a static black hole is described by a Schwarzchild metric

charged black holes are described by the Reissner–Nordström metric
rotating black holes are described by the Kerr metric
black holes with both charge and angular momentum are described by Kerr–Newman metric

Now, let’s add a little quantum physics to this classical point of view. Even if nobody really knows how gravity can be incorporated into quantum mechanics, in the quiet zone, gravitational effects can be weak enough for calculations to be reliably performed in the framework of quantum field theory in curved spacetime.

Hawking showed that quantum effects – and contrary to what classical general relativity predicts – can allow black holes to emit radiations. For this, one has to think first about the quantum vacuum.

The quantum vacuum is the quantum state with the lowest possible energy. Contrary to one could expect, it all but a simple empty space. At the heart of quantum mechanics lies the Werner Heisenberg‘s uncertainty principle. It is the formalization of the fact it is not possible to measure simultaneously the value of pairs of quantum variables with certainty. The standard deviations $(\sigma_p , \sigma_q)$ of such conjugated variables $(p , q)$ are connected through Heisenberg’s relations:

$\sigma_p \times \sigma_q \sim \frac{\hbar}{2}$

Applied to Energy and time, it gives : $\Delta E \times \Delta t \sim \frac{\hbar}{2}$

This means that during a very short period of times, there will be enough energy $E = m c^2$ to create a particle-antiparticle pair that would annihilate shortly after. The quantum vacuum can then be pictured as being filled with virtual particles popping into and out of existence :

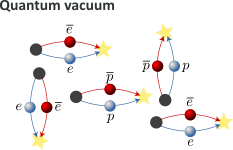
Following Yakov Zeldovich and Alexei Starobinsky, Steven Hawking and Jacob Bekenstein imagined a particle-antiparticle (virtual) pair to appear close to the event horizon of a black hole. One of the virtual pair “falls into” the black hole while the other escapes:

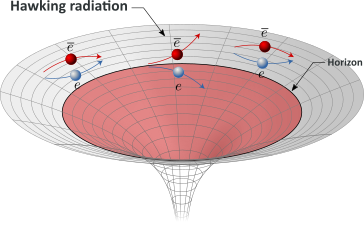
In order to preserve total energy, this causes the black hole to lose mass. For an outside observer, it would appear that the black hole has just emitted a particle : a real photon, produced via the annihilation of the remaining pair with another virtual (anti-)particle outside of the black hole. This process (which is in fact much more complex) is called Hawking radiation.

Through this process, a black hole would lose mass and eventually evaporate. The time for a black hole of mass $M_0$ to dissipate is:

$t = \frac{5120 \pi G^2 M^3_0}{\hbar c^4}$

This a slow process though, and black holes are huge. For a black hole of one solar mass, it would take more than current age of the universe…

This radiation is somehow paradoxical, because, as the no-hair state, a black hole is solely characterized by three external parameters (mass, electric charge and angular momentum). It means than form the outside, any information entering inside the black hole is kept stored inside. But as the black hole eventually evaporates, this information is ultimately lost. This information paradox ignited a 40 years long and heated debate (and a bet lost by Hawking in 2004) between renowned physicists Steven Hawking, John Preskill, Kip Thorne, Gerard ‘t Hooft and Leonard Susskind.

This battle between these friends and colleagues leaded to the holographic principle (and a later post will be dedicated to it), where the three dimensions of space could be reconstructed from a two-dimensional world without gravity – much like a hologram.

A few days ago, Hawking made a communication on that particular subject at the KTH Royal Institute of Technology. His idea is that information never actually makes it inside the black hole :“I propose that the information is stored not in the interior of the black hole as one might expect, but on its boundary, the event horizon […]”. His suggestion is that the information about particles passing through is translated into an hologram that would sit on the event horizon.

Using the holographic principal, one can describe the evaporation of the black hole in the two-dimensional world without gravity, for which the usual rules of quantum mechanics apply. This process is deterministic, with small imperfections in the radiation encoding the history of the black hole. Holography tells us that information is not lost in black holes, a priori solving the information paradox.

A paper will be published next month, fully describing the findings.

Although I’m not a great fan of string theories, one shall note that there are alternative descriptions of black holes which a priori solve the information paradox, like superstring fuzzballs – where singularity at the heart of a black hole is replaced by theorizing that the entire region within the black hole’s event horizon is actually a ball of strings.

As weird as they might be, black holes are not purely theoretical singular objects. By nature, black holes do not directly emit any signals other than the Hawking radiation, which is weak and difficult to measure. Nevertheless, indirect observation is possible because the interact of such massive objects with its environment (accretion of matter, gravitational lenses, …)

Although we do not fully understand black hole physics (absence or presence of singularities, Hawking radiation, evaporation, information paradox, …), there is a full list of candidates.

White holes

White holes possible existence was put forward by Igor Novikov as part of a solution to the Einstein field equations. A white whole is, roughly speaking, the opposite of a black hole. According to Sean Carroll : “A black hole is a place where you can go in but you can never escape; a white hole is a place where you can leave but you can never go back. Otherwise, [both share] exactly the same mathematics, exactly the same geometry.”

White hole existence outside equations is nevertheless highly speculative, though some think the big bang is somehow a while hole.

Some also have proposed that when a black hole forms, a big bang may occur at the core, which would create a new baby universe that would expands outside of the parent universe.

There is no known observation corroborating the existence of white holes and white hole theories are shaky. All this has to be taken with a huge grain of salt.

Wormholes

Lorentzian wormholes (Einstein-Rosen bridges) are other typical singular objects. They which describe “shortcuts” connecting two separate points in space-time (even many light-years apart), different universes, or even different points in time. In a 2-dimensional surface, a wormhole would appear as a hole in that surface, lead into a world-tube, then re-emerge at another location on the 2-dimensional surface with a similar hole. An actual wormhole would be analogous to this, but with the 3 spatial dimensions. The entry and exit points would be visualized as spheres in 3-dimensional space. The possibility of traversable wormholes in general relativity was first demonstrated by Kip Thorne.

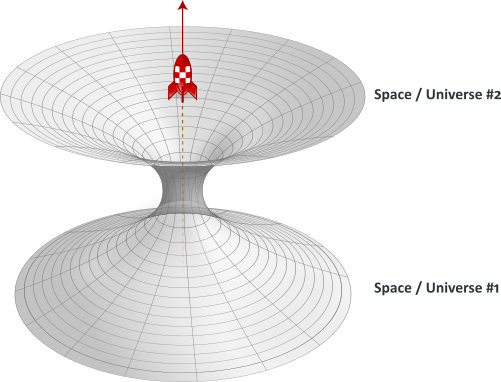
Wormholes lead to many paradoxes and introduce non-linearities at the quantum level. David Deutsch nevertheless showed that time paradoxes can be solved within the many-world interpretation of quantum mechanics, where a particle returning from the future would not return to its universe of origination but to a another world. String theorist Joseph Polchinski discovered an “Everett phone” (a theoretical universe-to-universe communicator) in Steven Weinberg’s formulation of nonlinear quantum mechanics. Such a possibility (and a scientifically correct visualization of spherical 3-dimensional wormhole entrance) is depicted in Christopher Nolan‘s remarkable film Interstellar. But from what we know, there is no observation corroborating the existence of wormholes, which remains hypothetical.

Horizons

Horizons are boundaries in space-time beyond which events cannot affect an outside observer (and conversely, the observer cannot affect these events).

We have already seen how Einstein’s special relativity defines a causal structure. If at a given event E (that will be called “present” for the observer) a flash of light is emitted, it will expend at the speed of light in the form of a growing sphere. Since nothing can go faster than the speed of light, this expanding sphere is a boundary beyond which nothing affects or can be affected by E.

If one tries to visualize this sphere of light in a 3-space where two horizontal axes are chosen to be spatial dimensions and the vertical axis is chosen to be time, the expending light-sphere will be represented by an expending circle, which, as time go, will span a light-cone centered on the event E :

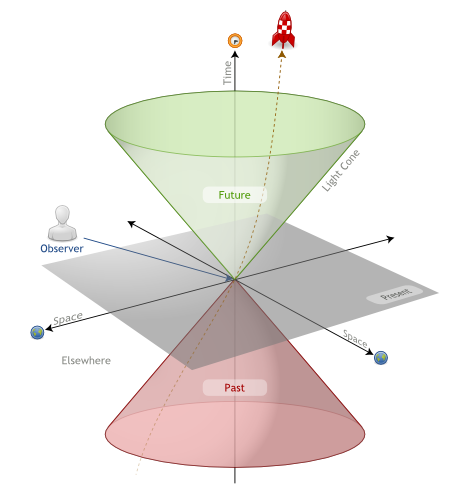
Relatively to the event E, the light cone will classifies event into distinct areas:

The green light cone defines the future: events affected by information emitted at E
The red light cone defines the past: events than can affect the present
All other events are in the absolute elsewhere: events that cannot effect or be affected by E

The above classification holds true in any frame of reference. An event judged to be in the light cone by one observer, will also be judged to be in the same light cone by all other observers, no matter their frame of reference.

Now let’s introduce gravity.

The good old flat (pseudo)-minkowskian space-time will, under the influence of gravity, transforms into a curved (pseudo)-riemanian space-time. The curvature of space-time will be depicted by the tilting of the lightcones. The causal structure around a star will then be depicted as follows :

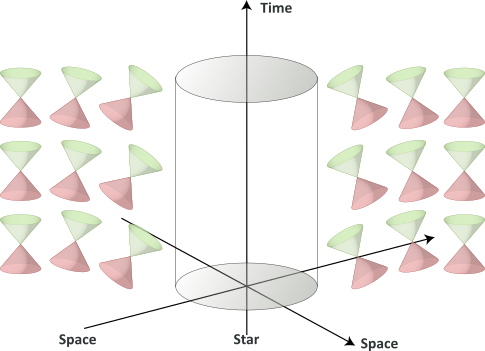
When the star collapses into a black hole, the curvature of space-time becomes so severe that, for some region, there is no path out of that region that remains inside its own light-cones. That is, the causal structure of the space-time is such that one cannot escape from that region :

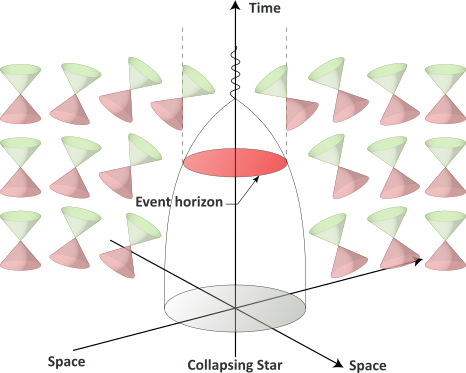
The border of that region (in red in the above illustration) is called the black hole event horizon. The surface at the Schwarzschild radius acts as an event horizon in a non-rotating body that fits inside this radius (although a rotating black hole operates slightly differently).

Black hole event horizons are often misunderstood. A common error is the idea that matter can be observed “falling into” a black hole. This is not possible, precisely because no information exits from the horizon. Astronomers can only detect accretion disks around black holes, where material moves with such speed that friction creates high-energy radiation which can be detected, outside of the black hole.

Black hole event horizons are not the single type of event horizons.

Let’s introduce the notion of Hubble sphere. In cosmology, a Hubble sphere is a spherical region of the Universe surrounding an observer beyond which objects recede from that observer at a rate greater than the speed of light due to the expansion of the Universe (we will get into the universe expansion in the next paragraph).

Objects at the Hubble limit have an average proper speed equal to the speed of light relative to the observer. In a universe with constant Hubble parameter, light emitted at the present time by objects outside the Hubble limit would never be seen by the observer. That is, Hubble limit would coincide with a cosmological event horizon.

Now that the notion of event horizon has been a little bit precised (there are actually other types of horizons, like the apparent horizon), let’s think about realities hidden beyond these horizons.

As far as black hole horizons go, it would not be very interesting: if life or other worlds or universes would exist inside a black hole horizon, it would be hidden for good from what we know.

But, this actually include the singularity predicted by general relativity (but which might be ruled out by quantum physics), which is completely enclosed by the black hole event horizon. Actually, Roger Penrose proposed in the late seventies the Cosmic Censorship hypothesis: is postulates that no naked singularities (other than the Big Bang) exist. Nevertheless, loop quantum gravity suggests that this hypothesis does not hold. ohn Preskill and Kip Thorne bet (again …) against Stephen Hawking that the hypothesis was false. The bet was conceded by Hawking.

The cosmological event horizon is even funnier, because the Hubble parameter is not necessary constant. In many cosmological models, the Hubble limit does not coincide with a cosmological event horizon.

For example in a decelerating universe, the Hubble sphere would expand faster than the universe and its boundary would overtake light emitted by receding galaxies. Light emitted at earlier times by objects outside the Hubble sphere would would eventually arrive inside the sphere and be seen by us. Unseen “universes” would then appear to us.

Conversely, in an accelerating universe, the Hubble sphere expands more slowly than the Universe, and bodies move out of the Hubble sphere. And actually, observations indicate that the universe is accelerating. Thus, some objects that we can currently exchange signals with will one day cross our Hubble limit. They would disappear to us (or conversely, we would disappear to them).

Relativistic cosmology

Physical cosmology is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its origin, structure, evolution, and ultimate fate.

Let’s start with the large-scale structure of space-time and consider a simple space-time model such as Friedmann’s. In this model, space-time is an homogeneous and isotropic expanding universe and the overall curvature of the universe is governed by the density parameter $Ω$ :

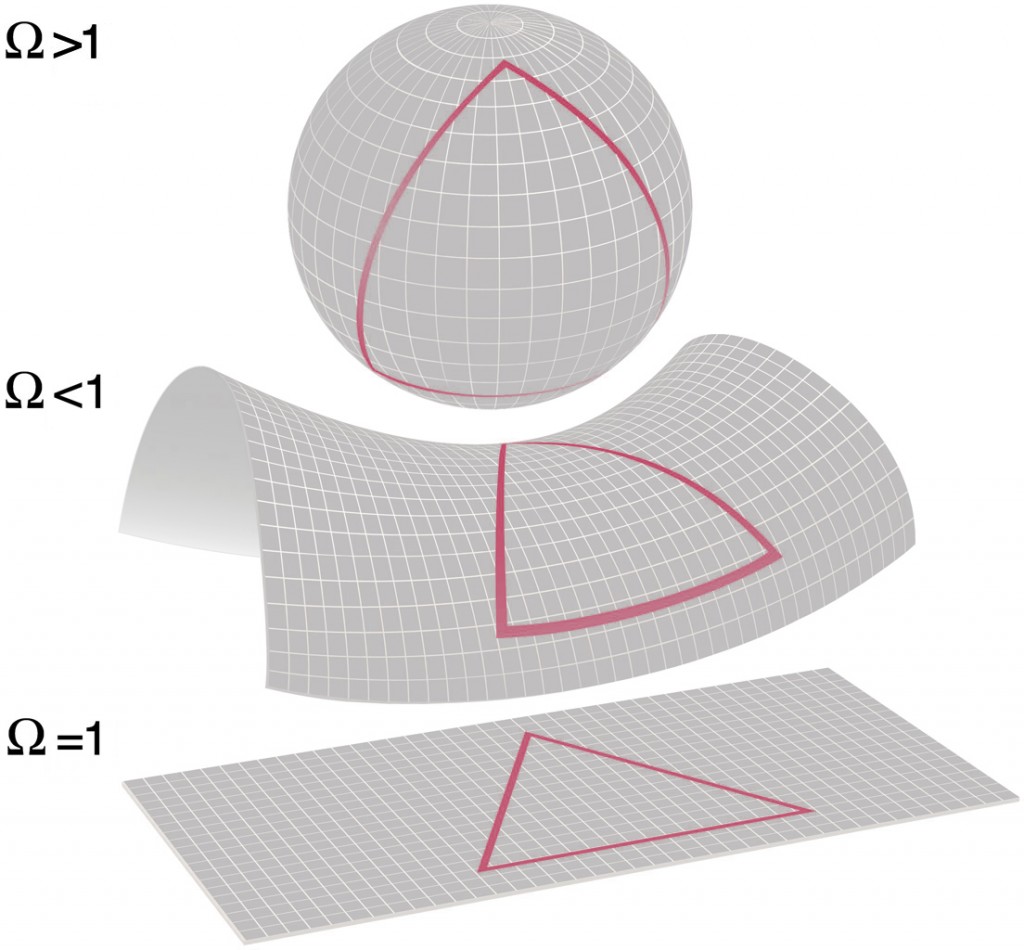
If $Ω > 1$ , the global curvature of the universe is positive
if $Ω < 1,$ the global curvature of the universe is negative
If $Ω = 1$ , the universe is flat

The density parameter $Ω$ can actually be experimentally measured. Data from the Wilkinson Microwave Anisotropy Probe (see below the image of the cosmic microwave background measured by WMAP, from which is $Ω$ evaluated), the Planck spacecraft or the BOOMERanG experiment indicate that $Ω ~$ 1.00

From these measured values, it seems that within experimental error, the universe is globally flat. Which is kind of boring. But kind of only, because observations do not say anything about how those volumes fit together to give the universe its overall shape – its topology.

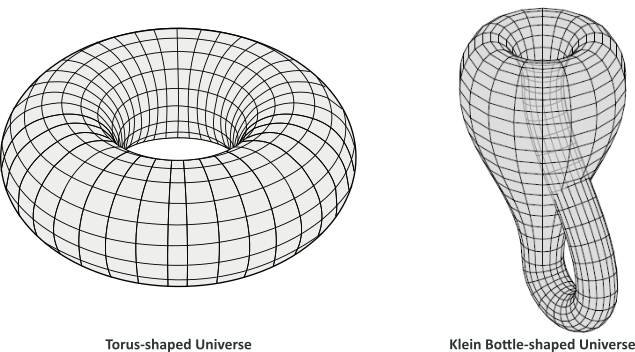
In a universe with zero curvature, the local geometry is flat. The most obvious global structure is that of Euclidean space, which is infinite in extent.

In three dimensions, there are 10 finite closed flat 3-manifolds, of which 6 are orientable and 4 are non-orientable. Flat universes that are finite in extent include the torus and Klein bottle:

Of course, other possible shapes have been proposed, like Jean-Pierre Luminet‘s proposal that the shape of the Universe is a finite dodecahedron, attached to itself by each pair of opposite faces, forming a Poincaré homology sphere. As beautiful as this proposal may be, there is no strong support for the correctness of the model, as yet.

How comes the universe is so flat ?

The inflationary hypothesis was initially proposed by Alan Guth in the early 1980s. It explains the origin of the large-scale structure of the cosmos. The idea that the universe went through a brief period of exponential expansion in the first fraction of a second after the Big Bang; the flatness problem and the horizon problem (along with the along with the monopole problem, which is a different subject) are three principal motivations for inflationary theory.

The detailed quantum mechanism responsible for inflation is not known, Nevertheless, the basic picture makes a number of predictions that have been confirmed by observation. The hypothetical field thought to be responsible for inflation is called the inflaton. Some think it is related to the Higgs field.

The horizon problem is easy to understand. It points out that different regions of the universe have not “contacted” each other because of the great distances between them (as we’ve seen with the Hubble sphere), but nevertheless they have the same temperature and other physical properties. This should not be possible, given that the transfer of information (or energy, heat, etc.) can occur, at most, at the speed of light…

Inflation answers this question by postulating that all the regions come from an earlier era with a cosmological constant (big vacuum energy). Space with a cosmological constant is qualitatively different: instead of moving outward, the cosmological horizon stays put. For any one observer, the distance to the cosmological horizon is constant. With exponentially expanding space, two nearby observers are separated very quickly; so much so, that the distance between them quickly exceeds the limits of communications. Things are constantly moving beyond the cosmological horizon, which is a fixed distance away, and everything becomes homogeneous very quickly.

Dark energy is the most accepted hypothesis to explain the observations since the 1990s indicating that the universe is expanding at an the accelerating rate astronomers are measuring when observing the light from distant galaxies and supernovae.

In the absence of dark energy, a flat universe expands forever but at a continually decelerating rate, with expansion asymptotically approaching zero. With dark energy, the expansion rate of the universe initially slows down, due to the effect of gravity, but eventually increases. As the inflationary field slowly relaxes to the vacuum, the cosmological constant goes to zero, and space begins to expand normally. The new regions that come into view during the normal expansion phase are exactly the same regions that were pushed out of the horizon during inflation. Thus they are necessarily at nearly the same temperature and curvature, because they come from the same little patch of space.

If the theory of inflation explains why the temperatures and curvatures of different regions are so nearly equal, it also predicts that the total curvature of a space-slice at constant global time is zero. Irrespective of the original geometry of the Universe, it would appear flat to us. The analogy will be to take a balloon; we can easily see it to be rounded; now blow the balloon to a very large volume and then put a small ant on its surface. The ant will think that it is on a sheet; it cannot detect the curvature.

The ΛCDM (Lambda cold dark matter) has become the standard model of big bang cosmology.

It assumes that general relativity is the correct theory of gravity on cosmological scales and is the simplest model that provides a reasonably good account of the following properties;

the existence and structure of the cosmic microwave background
the large-scale structure in the distribution of galaxies
the abundances of hydrogen (including deuterium), helium, and lithium
the accelerating expansion of the universe

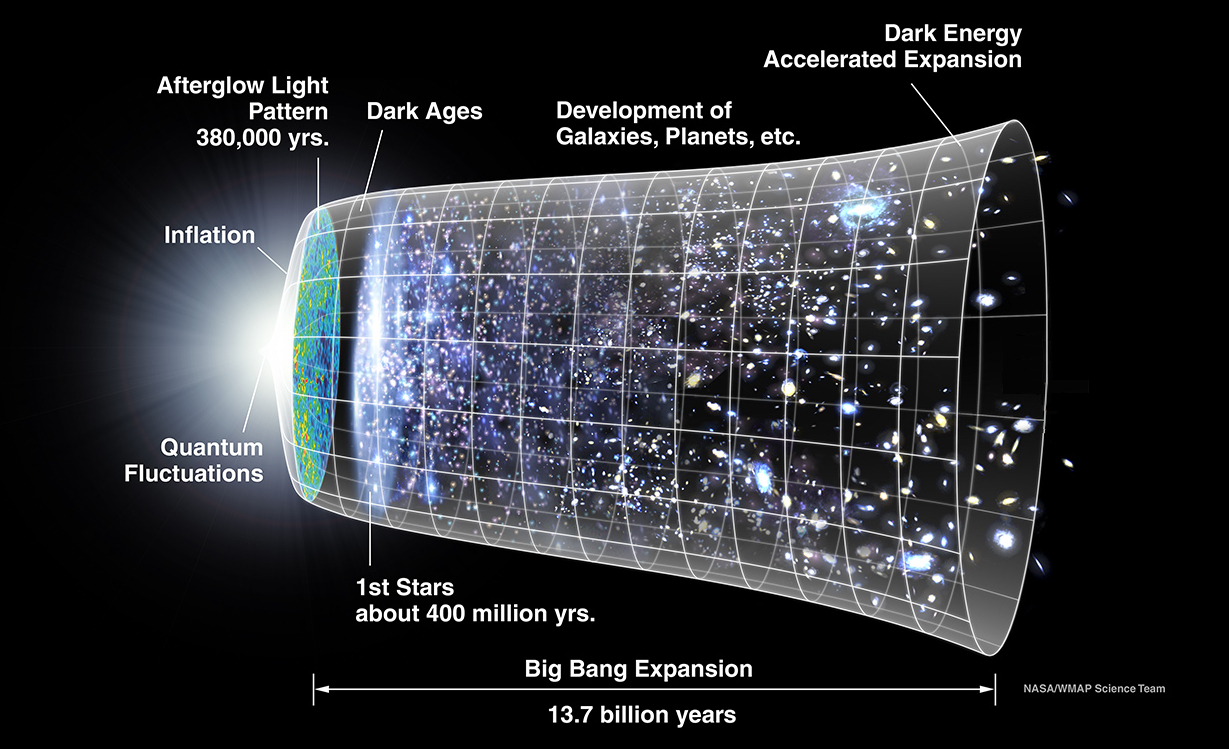
The following illustration pictures the evolution of the universe according to this model:

Cyclic universe

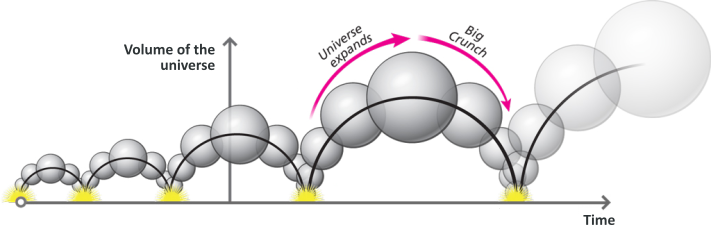
Cyclic cosmological models theorize that the universe follows self-sustaining cycles. For example, the oscillating universe theory briefly considered by Albert Einstein in 1930 described a universe following series of oscillations, each beginning with a big bang and ending with a big crunch. Between cycles, the universe would expand until gravitational attraction causes it to collapse back and undergo a big bounce.

But these early attempts failed because of the cyclic problem: according to the Second Law of Thermodynamics, entropy can only increase. This implies that successive cycles grow longer and larger. If we go back in time, cycles before the present one would become shorter and smaller, culminating again in a … big bang and … thus not replacing it.

Several alternative cyclic universe have since been proposed:

Conformal cyclic cosmology – a general relativity based theory proposed by Roger Penrose. In this model, the universe expands until all the matter decays and is turned to light – so there is nothing in the universe that has any time or distance scale associated with it. This permits it to become identical with the Big Bang, so starting the next cycle.
Loop quantum cosmology which predicts a “quantum bridge” between contracting and expanding cosmological branches.

Perpetual Inflation

In perpetual inflation models proposed by physicists like Alan Guth or Andrei Linde, the inflationary phase of the universe’s expansion lasts forever in at least some regions of the universe. Because these regions expand exponentially rapidly, most of the volume of the universe at any given time is inflating. All models of eternal inflation produce an infinite (fractal) multiverse. In these interpretations, new universes would pop into existence (at unknown rate), creating a complex web of bubble universes within a larger multiverse.

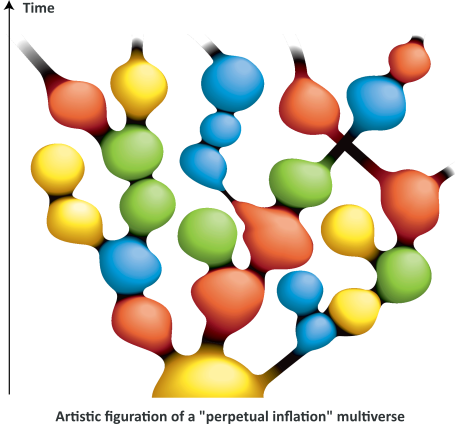
New inflation does not produce a perfectly symmetric universe: tiny quantum fluctuations in the inflaton are created. These tiny fluctuations form the primordial seeds for all structure created in the later universe. These fluctuations were calculated by four groups of physicist working separately (over the course of a workshop), including Stephen Hawking, Alan Guth. Even if these models turns out to be consistent with WMAP data adds weight to the idea that the universe could be created in such a way, many physicists agree it is possible, but needs further work and data support to be accepted.

Poetic ending

Let’s, once again, end this post on a poetic note. As mentioned above, Christopher Nolan‘s film Interstellar is truly remarkable.

From an artistic point of view the film – in its narration and its aesthetic – can be seen as a beautiful offspring of Stanley Kubrick‘s masterpiece 2001: A Space Odyssey.

From a scientific point of view, it is probably one of the most accurate film I have ever seen (depiction of black holes and wormholes, time stretching, naked singularities, “Everett phone”, …), thanks to Kip Thorne’s implication in the making of the film.

Leave a Reply Cancel reply