Quantum teleportation – Quantum Bits

In this new post on quantum computing, we are going to talk about quantum teleportation. Teleportation. OMG. Yes, I can see those stars sparking in your geeky eyes …

So … first, let’s clarify a few things, shall we ?

Quantum teleportation is a communications protocol that transfers the quantum state of a system to another spatially separated system. For this, it takes advantage of quantum entanglement. Contrary to what the name suggests, it is not a matter of transferring matter (or energy).

Quantum teleportation is defined as a process by which a quantum bit can be transmitted from one location to another, without the quantum bit actually being transmitted through space

So, although the name is inspired by the teleportation commonly used in fiction, quantum teleportation is not a form of transportation, but a form of communication.

Please stay. I won’t tell Captain Kirk. And Mr Spock would be so proud of you he could smile.

Note: for a short introduction to quantum bits and quantum computing, please follow this link (quantum computing) and this link (EPR, entanglement and Bell states)

The seminal paper first expounding the idea of quantum teleportation was published by C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres and W. K. Wootters in 1993.

Quantum teleportation requirements are:

Two locations A and B (Alice and Bob),
The ability to create an entangled EPR pair
A conventional communication channel, used to carry classical bits,
A quantum channel, used to send qubits from the entangled pair to A and B

The protocol goes as follows:

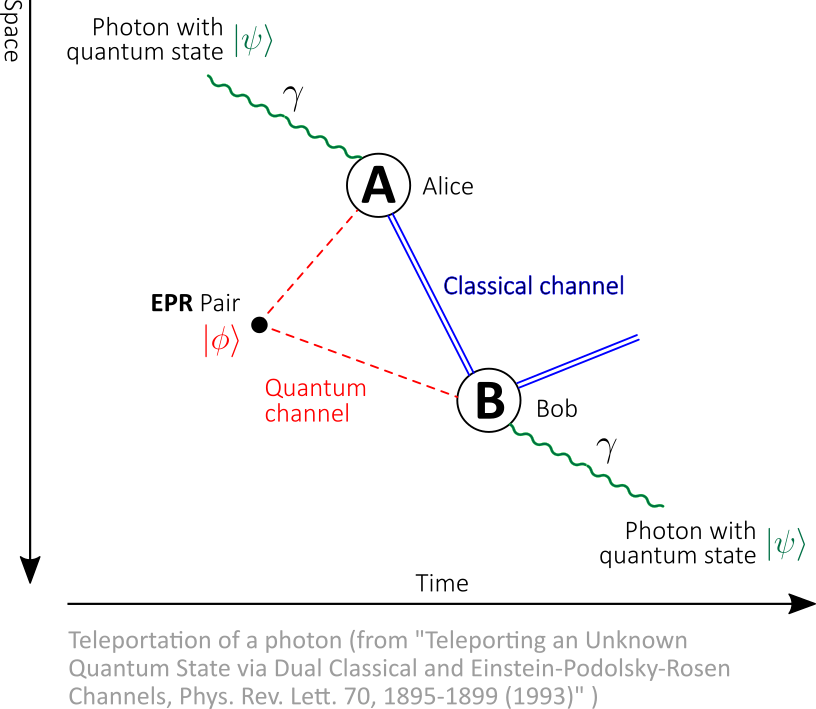
The teleportation protocol begins with a quantum state $|\psi\rangle$ , in Alice’s possession. The purpose of the teleportation is to convey $|\psi\rangle$ from Alice to Bob.

Generally speaking, this qubit can be written as: $|\psi\rangle = \alpha |0\rangle + \beta |1\rangle$ .
Next, the protocol requires that Alice and Bob share a maximally entangled state. It can be any one of the four Bell states (it doesn’t matter which one).

Let’s say that Alice and Bob mutually agreed on: $|\phi\rangle = \frac{1}{\sqrt{2}} \big( {|0\rangle}_A \otimes {|0 \rangle}_B + {|1\rangle}_A \otimes {|1 \rangle}_B \big)$ .
Now, let’s assume that Alice and Bob are sharing the state $|\phi\rangle$ .
Through the quantum channel, Alice obtains one of the particles in the pair, with the other going to Bob. This can be implemented, for example, by preparing the particles together and shooting them to Alice and Bob from a common source.
At this point:
- Alice has two particles : $|\psi\rangle$ (the one that she wants to teleport), and one of the entangled pair (let’s call it A)
- Bob has one particle: the other part of the entangled pair (let’s call it B).
- A the global system level, the state is described by a three-particles quantum state:
  
  $\displaystyle |\phi\rangle \otimes |\psi\rangle = \frac{1}{\sqrt{2}} \big( {|0\rangle}_A \otimes {|0 \rangle}_B + {|1\rangle}_A \otimes {|1 \rangle}_B \big) \otimes \big( \alpha |0\rangle + \beta |1\rangle\big)$ .
Alice makes a local measurement on the two particles in her possession. Alice’s two particles are now entangled to each other. The result of Alice’s (local) measurement is that the three-particle state would collapse to one of the four possible states. The entanglement originally shared between Alice’s and Bob’s particles is now broken.

Experimentally, this measurement may be achieved via a series of laser pulses directed at the two particles.
Following the local measurement, Bob’s particle now takes on one of four possible superpositions. With a little math (expressing the quantum states in terms of the 4 Bell states basis), it is easy to show that these possible are unitary images of the qubits to be teleported.
The result of Alice’s Bell measurement tells her which of the above four states the system is in. Alice then sends her result to Bob through a classical channel (using two classical bits to communicate which of the four results she obtained). This is the only potentially time-consuming step, due to speed-of-light considerations.
After Bob receives the message from Alice, he knows then which of the four states his particle is in. Using this information, he can perform a unitary operation to transfer the state on its particle. Teleportation is thus achieved.

Please note that:

After this operation, Bob’s qubit will take on the state $|\psi\rangle$ and Alice’s qubit becomes an (undefined) part of an entangled state. Teleportation does not result in the copying of qubits, and hence is consistent with the no cloning theorem.
There is no transfer of matter or energy involved. Alice’s particle has not been physically moved to Bob: only its state has been transferred.
Every time a qubit is teleported, Alice needs to send Bob two bits of information thought the classical communication channel.These two classical bits do not carry complete information about the qubit being teleported.

If Eve (an eavesdropper) intercepts these two bits, she may know exactly what Bob needs to do in order to recover the desired state. However, this information is useless if she cannot interact with the entangled particle in Bob’s possession.

Quantum circuit

It is possible to express the previous quantum teleportation protocol in terms of quantum circuits. Typically, the unitary transformation that is the change of basis (from the standard product basis into the Bell basis) can be written using quantum gates:

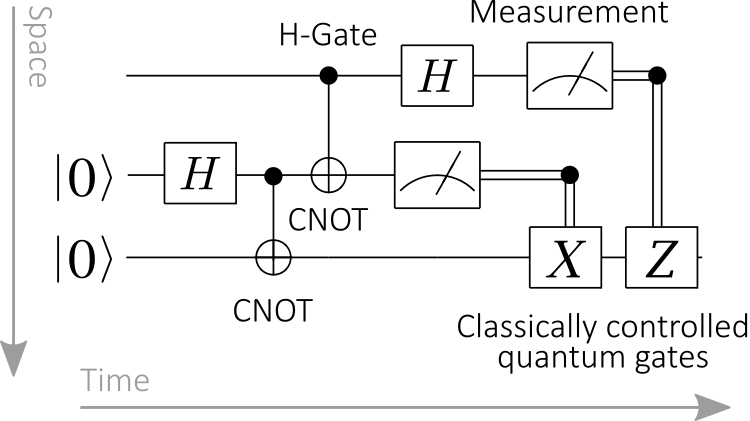
This quantum circuit will be used in the next paragraph, as the basis of a little quantum algorithm experimentation with the Q# language and its Quantum Development Kit.

Experimenting with Q#

We introduced the basic concepts of Q# in our last post on Bell states. Basic quantum teleportation code is provided as a sample in the Quantum Development Kit. Let’s have fun and follow it !

Let’s start with the non-quantum part of the program, used to invoke the quantum simulator, feed it with input data and read outputs from it:

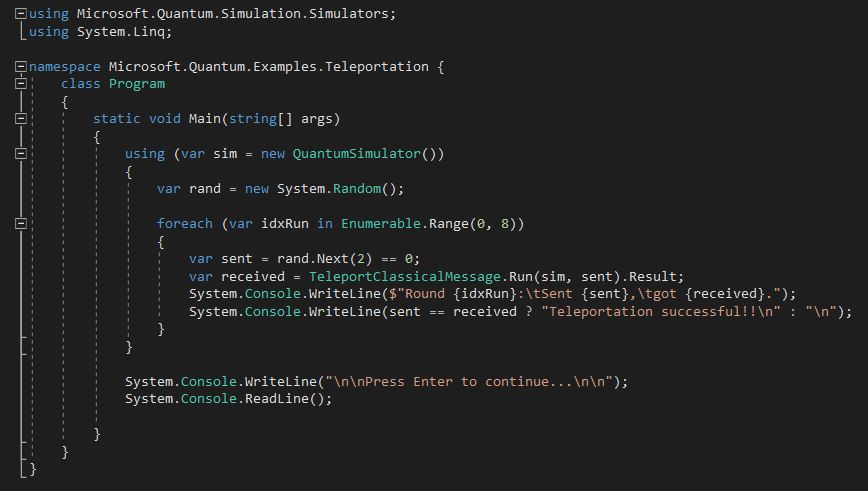
It is rather simple:

it invokes the quantum simulator,
it tries 8 quantum teleportations,
for each round, it randomly chooses the boolean value (either “true” or “false”) to be sent, then checks if this value has been properly teleported.

Now comes the quantum part of the program. As we have seen earlier on, two communication channels are required:

A classical channel (for classical data)
A quantum channel (for the entangled EPR pair)

The implementations are following the circuit for quantum teleportation introduced in the previous paragraph.

The code for the classical channel is:

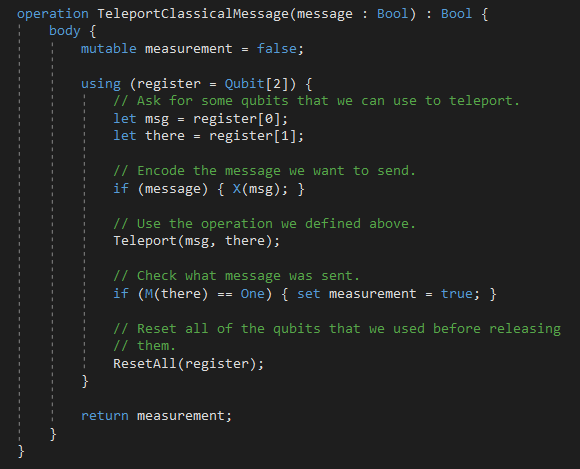
And the code for the quantum channel is:

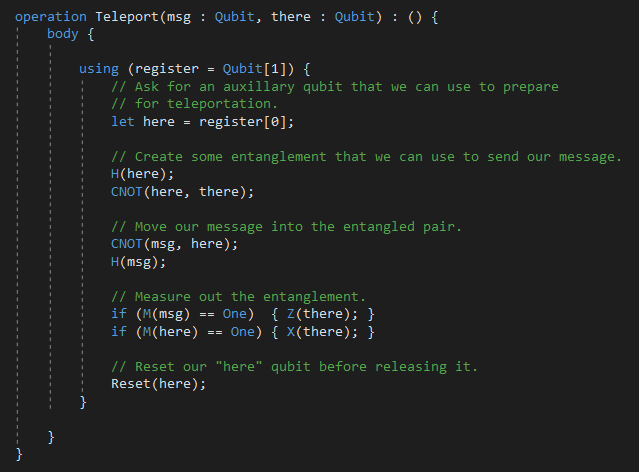
… and the results (outputs from the classical part of the program) are:

Great ! We have successfully teleported 8 boolean values 🙂

Importance of quantum teleportation

Since 1993, many real life quantum teleportation experiments have been carried out. First verifications came as early as 1998, and subsequently, the record distance for quantum teleportation has been gradually increased.

On 26 February 2015, scientists at the University of Science and Technology of China in Hefei, led by Chao-yang Lu and Jian-Wei Pan carried out the first experiment teleporting multiple degrees of freedom of a quantum particle. Later on (2017), the team achieved the first quantum teleportation from Earth to a satellite, while their counterparts in Japan are the first to use a microsatellite for quantum communications.

Masahide Sasaki and colleagues at the National Institute of Information and Communications Technology in Japan demonstrated in late 2017 that they were able to receive and process the information at a ground station in Japan using a quantum key distribution (QKD) protocol. QKD uses principles of quantum mechanics to ensure that two parties can share an encryption key secure in the knowledge that it has not been intercepted by a third party.

Quantum teleportation is a very active subject of research, with concrete applications to telecommunications and encryption.

Note: to speedup the writing of this post, a few paragraphs and illustrations are based on wikipedia’s entries on quantum teleportation. Q# code is based on MS Quantum Development Kit documentations and samples.

Leave a Reply Cancel reply